C#で数値計算:中心極限定理を確かめる
Mol には各種統計分布に対応した乱数発生クラス(RandomNumber)が用意されています。
そこで、RandomNumber（と統計処理クラス Stat）を利用して「中心極限定理(Central Limit Theorem)」を確認してみます。
乱数（RandomNumber）や統計処理（Stat）の詳細はリファレンスを参照してください。
中心極限定理
中心極限定理とは
平均値 μ で標準偏差 σ の母集団から十分大きい標本数 n の標本（xj, j=1,2,...,n）を繰り返し抽出して標本平均 Xi（i回目の抽出の場合）
Xi = (x1 + x2 + ... + xn)/n
を求める。
同じ標本数(n)の標本を繰り返し（N回）抽出して計算すると(X1,X2,...,XN)、
Xi（i=1,2,...,N） は母集団分布とは関係なく、平均 μ で標準偏差が σ/n1/2 の正規分布に近づく。
つまり、母集団の統計分布に関わらず、n を増やせば
- Xiの標本平均は、母集団の平均値 μ
- Xiの標本分散は、母集団の分散の 1/n（σ2/n、バラツキが狭くなる）
- Xiは平均値 μ 、標準偏差が σ/n1/2 の正規分布
に近づきます（i=1,2,...,N）。
※母集団に平均値と標準偏差（分散）が存在することが条件です。
確認方法
Mol の例題集の乱数計算例(FormRand)のソースコードを変更して、新たにフォーム(FormCLT)を作成します。
乱数の例では乱数発生回数は1回ですが、FormCLT では n 回発生させて Xi を計算します。
プログラムでは n はユーザが変更できます。その他、N = 2000 、乱数値の発生範囲を M(=100) 個に等分割して、各区間の出現頻度を計算します。
さらに、各区間の出現頻度を全区間の総出現頻度で割って、各区間の出現確率とします。
出現確率の折れ線グラフと、標本平均と標本分散を持つ正規分布のグラフ（描画オブジェクトとして MsChart:System.Windows.Forms.DataVisualization.Charting を使用しています）を同時に表示しています。
（本来は母集団の平均と分散を使用した正規分布グラフを描くべきですが…）
※詳細はソースコード(と実行モジュール)を参考にしてください。
プログラム（MolExamples.exe）を起動したら「Central Limit Theorem」ボタンをクリックして
- n の数を増やすとグラフの幅が狭くなると同時に正規分布グラフと重なります。
- 乱数の統計分布を変更しても、n を大きくすると同じように振る舞います。
- ただし、分散が定義されないコーシー分布はうまくあてはまりません。
を確認してください。
実行結果
まず、n = 1 の最初の画面です。乱数の分布関数は「一様分布」（デフォルト）です。
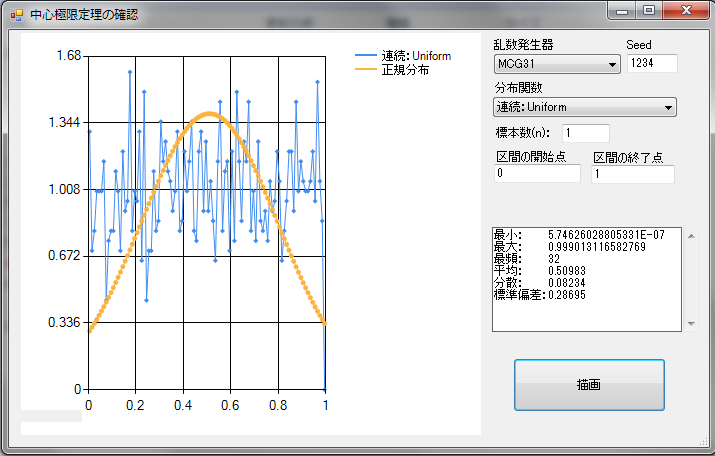次に、n = 2 の画面です。この時点で既にかなり正規分布に近づいています。
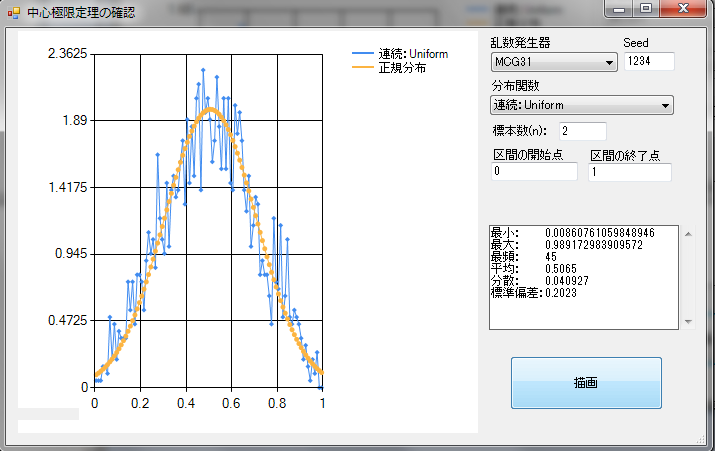最後に、n = 100 の画面で、バラツキが少ない尖った正規分布に重なっています。
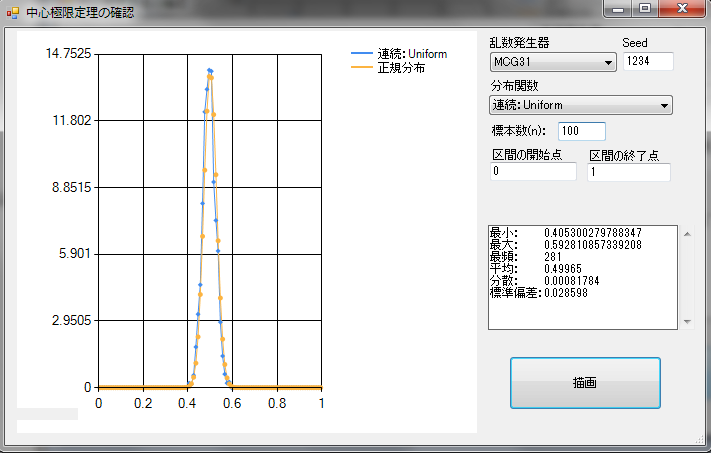同様に各種統計分布を試してみてください。大体似たような結果が得られます。
