Dsl (Digital Simulation Library) for .Net

前の章 （変数に属性を設定する） で「<T>(目的値)指定」や「ループの検出」で（連立）代数方程式を解く必要があることを記しました。 ここでは「連立方程式」の組み立てについて説明します。

このトピックスは以下のセクションを含みます。

連結成分

連結成分の分割
連結成分とは一連の変数が接続しているグループのことです。 接続関係を定義した因果関係定義段階でお互いに接続関係を持たない変数のグループは異なる連結成分に属することになります。

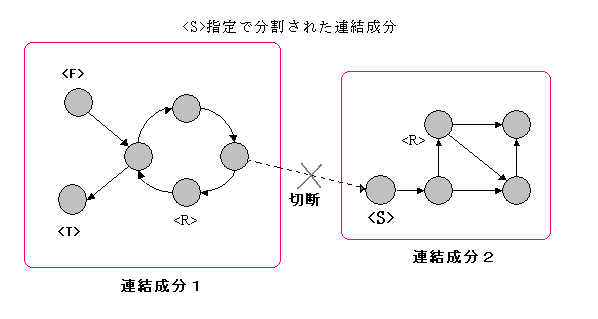
さらに、<S>型や<T>型（<I>型も同様）指定をした段階で接続関係が切断され、さらに異なる連結成分に分割されるのが普通です。

注意事項：

<R>型変数を含まない連結成分は処理から外されます。 以下の連立方程式解法の条件等は全て連結成分毎に成立することが必要です。

先頭へ

連立方程式と独立変数の関係

<F>-<T>対応
「<T>指定」された変数があれば方程式(一般に非線形連立)を解く必要があります。 当然のことながら<T>指定された変数の値を指定された値にするために、 上流には値を自由に調節できる独立変数（<F>型変数）が必要です。 <F>型変数は「値を自由に調節」できなければいけないので「右辺変数を持たない変数」です。 <F>型変数は自動的に検出され FLAG.FREE のフラグが設定されます。

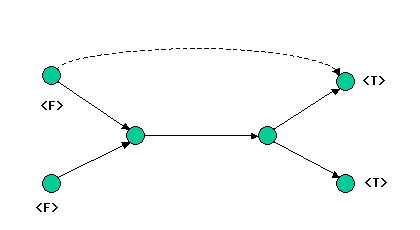
連立方程式が解けるには、以下の条件が必要です。

  1. 式の数(<T>型変数の数)と独立変数の数(<F>型変数の数)が等しい

  2. <F>型変数から<T>型変数に到る「独立した」ルートが存在

上図では点線のようなルートが存在しないと、途中でルートが重なるので方程式を解くことはできません（グラフ処理段階でチェックできます）。 もちろん、独立したルートが存在しても、それだけで「数値的に解けること」を保証するわけではありません。

<F>型変数は右辺変数を持たず、<S>型でもないので予め見当をつけるのは容易です。 <F>型変数は連立方程式の独立変数ですので、なるべく解に近い値を初期値として Value プロパティに値を設定しておくことが重要です。

先頭へ

ブロック三角化

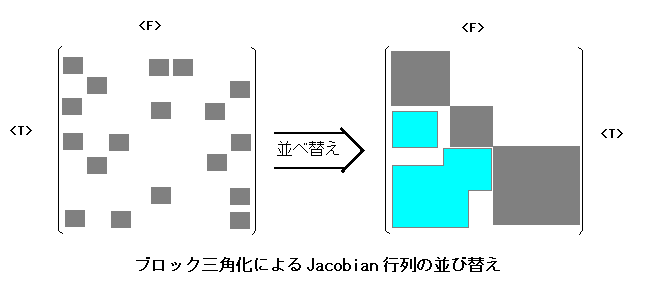
連立方程式の解法は Newton 法が用いられます。 Newton 法の場合、Ax = b という形の線形連立方程式を繰り返し解くことになります。 ここで A は Jacobian 行列で、各要素は<T>型変数を対応する<F>型変数で微分したものとなります。 もし、<T>型変数と<F>型変数が無関係なら対応する要素は常にゼロです。 <T>型と<F>型のペアが多数になれば、当然(大型の)連立方程式になります。 このような連立方程式を直接解くのは効率的とはいえません。 見た目が大型でも、実は小さな連立方程式を順序に従って解くことで同じ結果を得ることができる場合が多いのです。 このように「大きな連立方程式を、連続した小連立方程式に分割」することを「ブロック三角化」と呼びます。

ブロック三角化
上図では、バラバラな部分要素を並べ替えることによって大きな連立方程式が連続した３つの小連立方程式に分解されることを模式的にしたものです。 左下の薄い色の部分は小連立方程式の計算には寄与しないことになります。 さらに、個々の（小）連立方程式を効率よく解くために[Sparse行列専用解法]も用意されています。

Sparse行列専用解法

Jacobian 行列の全要素に対する非ゼロ要素の数が指定された割合(Processor の SparseCriteria プロパティ) を下まわると（非ゼロ要素の少ない行列を Sparse行列 と呼びます）、Sparse行列専用の解法に自動的に移行します。 Sparse行列専用解法では値がゼロである微分要素はメモリーを割り当てることも計算もしないので非常に効率が良くなります。
注意事項：
Dsl では Jacobian 行列要素は「数値微分」によって計算されます。従って面倒な解析微分式を用意する必要はありません。

先頭へ

参照

先頭へ