Dsl (Digital Simulation Library) for .Net

前の章 （因果関係と有向グラフ） では計算順序に従って Processor が計算を実行するということを記しました。 ここでは「計算順序」がどのような手順で決定されるのかを説明します。

注意事項：
計算順序は変数に与える属性(Flag)によって変わります。

このトピックスは以下のセクションを含みます。

変数に属性を設定する

「変数に属性を設定する」とは変数の Flag プロパティに USERFLAG の値を設定することです。

注意事項：
変数の属性にはユーザが設定する USERFLAG と Prosessor が設定する FLAGがあります。 ユーザは変数に特定の FLAG が設定されているか調べることはできますが、設定することはできません。 USERFLAG は FLAG のサブセットとなっています。

先頭へ

<R>(出力:USERFLAG.REQUIRED)指定

計算は結果を出力しなければ意味がありません。 従って「計算結果」を出力してほしい変数に <R> 型のフラグを与えます。 すると「<R>型のフラグを付けた変数と、その計算に寄与する変数」以外は無視されます。 従って、<R>型の変数が一つもなければ計算そのものが実行されないことになります。 例えば、z の値が必要（「計算結果」を出力してほしい）ならば以下のように、 z の Flag プロパティに USERFLAG.REQUIRED を設定します（Flag プロパティには他にもいくつかのフラグを | で連結して設定できます）。

 コピー　イメージコードをコピー
// z に<R>型フラグを設定する。
z.Flag = USERFLAG.REQUIRED; // z.SetFlag(USERFLAG.REQUIRED); でも可（違いはヘルプを参照のこと）
参照：SetFlag(USERFLAG)

先頭へ

<S>(定数:USERFLAG.SET)指定

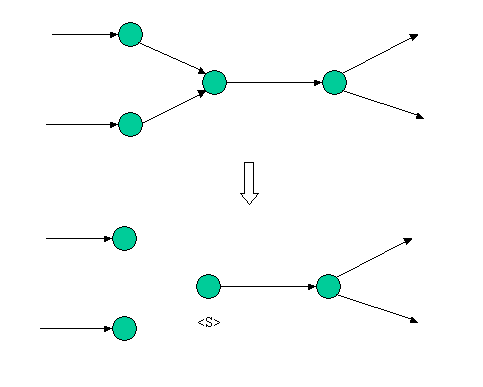
<S>型指定の結果

値が確定していて、わざわざ計算する必要のない変数に設定します。 この設定の結果、<S>型のフラグを持った変数に入る矢印はすべて取り除かれます。

注意事項：
つまり、因果関係と有向グラフ の時点で右辺変数を定義して、さらに ComputeValueAt プロパティを設定していても計算中に呼ばれることは無くなります。
 コピー　イメージコードをコピー
// z に<S>型フラグを設定する(値は1.0)。
z.Flag = USERFLAG.SET;
z.Value = 1.0;
チップ：
値は「計算されない」ので、当然、確定している値を予め Value プロパティに設定する必要があります。

先頭へ

<T>(目的値:USERFLAG.TARGETED)指定

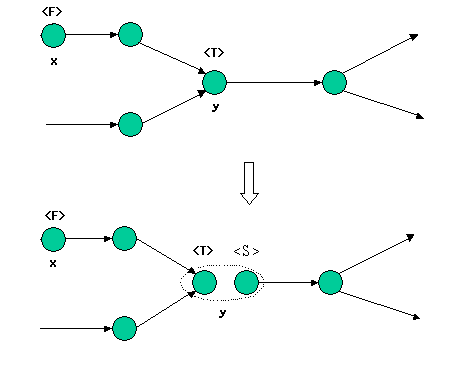
<T>指定の結果

ある特定の値に(計算の結果として)なって欲しい変数に設定します。

チップ：
特定の値を予め Value プロパティに設定する必要があります。
<T>型変数を y とすれば、y を所望の値にするために自由に値を調節できる（<F>:FLAG.FREE 型） 変数が y の右辺（上流）に必要です。 関数表現では
y = f(x)
としたときに、y に <T>型のフラグ(値は w)を付けると
y-w => 0.0
つまり
f(x)-w => 0.0
という x に関する方程式を解かなければいけないことになります。 独立変数（<F>型変数） x は値を調節できなければいけないので、右辺変数を持つことはできないし <S>型変数などの固定した値を持つことも出来ません（<F>型変数はグラフ処理時に Processor が決定します）。 複数の<T>型指定があれば、一般に(非線形)連立方程式を解くことになります。連立方程式の解法は Newton 法が用いられます。 従って<F>型変数に予め（解に近い）初期値を与えることが重要です。 また、ｙ を右辺として持つ変数は y の「特定の値」をそのまま使用すればいいわけですから、y を右辺に持つ他の変数からみれば y は <S>型に見えます。
 コピー　イメージコードをコピー
// y に<T>型フラグを設定する(値は1.0)。
y.Flag = USERFLAG.TARGETED;
y.Value = 1.0;
// <F>型の x に初期値を与える(値は0.1)。
x.Value = 0.1;
注意事項：
数式処理システムなら y=f(x) を x = g(y) という形に式を変形することで単純な計算にできる場合もありますが、 Dsl は式を変形する代わりに y-f(x)=>0 を x について解きます。

先頭へ

<I>(積分:USERFLAG.INTEGRATED)指定

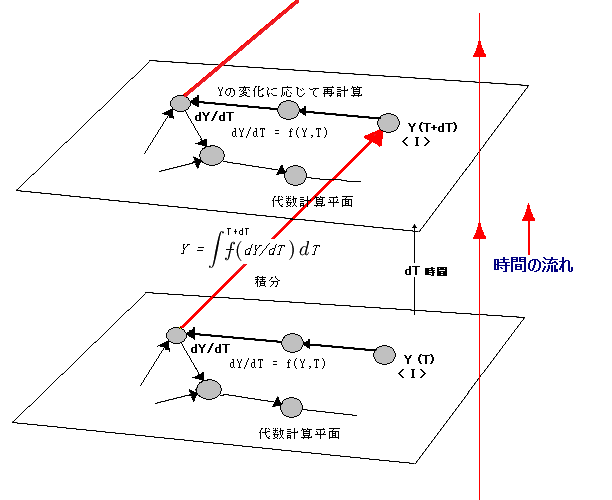
特定時間平面と積分の関係

<I>型指定された変数は「積分によって計算される」という意味になります。 <I>型変数の右辺変数は自動的に<DR>（微分）変数とみなされます。 <I>型変数の値は微分方程式を解くことで確定します。特定の時間平面では <S> 型と同じように定数として扱われます。 上図の赤い矢印が Y = Integral(dY/dT) の関係を表します。同時に、特定の時間平面（代数計算平面）上では、dY/dT = f(Y,T) という関係があるのが普通です。 通常のグラフ処理は一つの（特定の時間における）代数計算平面上の関係を扱いますが、<I>型指定は時間の流れに沿って過去と現在（現在と未来）の変数関係を定義するという意味でやや特殊です。

注意事項：
<I>型変数の右辺変数は自動的に微分型変数とみなされます。 <I>型変数一個につき微分型変数一個（<I>型変数の右辺は一個）としてください。 こうしないと、後述の定常状態の計算で不都合が生じます。
微分方程式の解法は

  • RUNGE-KUTTA(ルンゲ・クッタ法)

  • EULER(オイラー法)

  • BACKWARD-EULER(バックワード・オイラー法)

と３種類の解法が用意されていますので、<I>型指定された変数には ComputeValueAt プロパティを設定する必要はありません（設定して独自の解法を組み込むことも可能です）。
 コピー　イメージコードをコピー
Processor pr  = new Processor();
Variable dYdT = new Variable(pr,"dY/dT"); // 右辺の微分変数
Variable Y    = new Variable(pr,"Y");     // <I>（積分）型変数
Y.AddRightSideVariables(dYdT);            // Y = Integral(dY/dT) （Y は dY/dT を積分するという意味）
Y.Flag = USERFLAG.INTEGRATED;             //  <I>（積分）型指定
注意事項：
オイラー法とルンゲ・クッタ法はいわゆる「陽解法」です。バックワード・オイラー法は「陰解法」です。どちらも、 ある時刻 t での<I>型変数の値は決定しています（最初の値は初期値として与える必要があります）。
陽解法では、特定の時間平面上では値が決定（固定）している<I>型変数に影響される全変数をまず計算します。 次に、<I>型変数（のみ）が積分されて時間変化し、 その変化に合わせるために（次の時刻の）全変数が計算されます。 このように陽解法は代数計算と積分（時間の進み）が交互に実行されます。 これに対し、陰解法のバックワード・オイラー法は、上図下の時間面（時間T）の代数計算中に上の時間面（dT時間後）のY(T+dT)まで含んだ形でグラフ処理が適用されるという点で特殊です。

最も簡単なオイラー法とバックワード・オイラー法を比較すると以下のようになります。

　 dY/dT = f(Y,T) ... Tは時間
としたときに

オイラー法は

　 Y(T+dT) = Y(T) + f(Y(T),T)*dT
と計算されます。

ところがバックワード・オイラー法では

　Y(T+dT) = Y(T) + f(Y(T+dT),T)*dT ... 未知のY(T+dT)が両辺に含まれる。
という形になります。

この場合、左辺と右辺にY(T+dT)があるのでループになり、グラフ処理時点で<F>-<T>に分割されて、 代数方程式中に積分計算が組み込まれることになります。 つまり、陰解法では代数方程式計算が終了した時点で積分（次の時刻のYの値の計算）も完了します。

先頭へ

<DD>（ループ分割:USERFLAG.DIVISIBLE）型

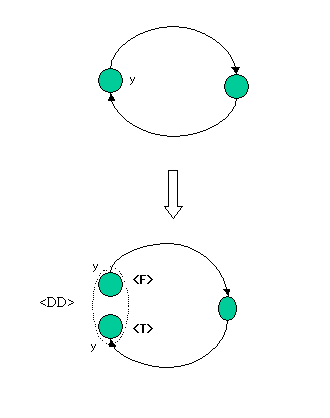
ループの処理

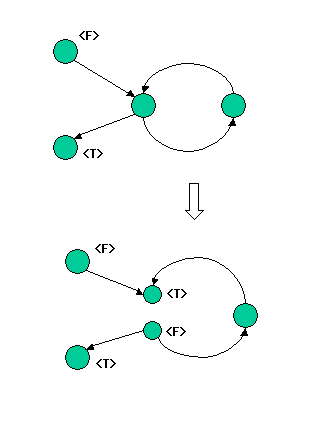
自分を計算するために「自分」が必要な場合。つまり、関数で表現すれば

y = f(y)
というような関係を「計算ループ」と呼びます。Processorは、このような計算ループを自動検出します。 さらに計算ループ上の変数(特に指定が無ければProcessorが決定します)を<F>型変数と<T>型変数に分割します。 分割された変数は<DD>型変数と呼ばれ FLAG.DIVIDED のフラグが Processor によって設定されます。

注意事項：
<DD>型の属性は先の<F>型の属性と同じように Processor が設定するという意味で若干特殊です。
y が<DD>型変数に設定されると
y=f(y)は yt = f(yf) => yf つまり yt - yf => 0.0
という形に変形(yt は値 yf の<T>型、yf は<F>型)処理されます。
チップ：
分割された元の変数 y は<F>型(yfで属性はFLAG.DIVIDED_F)となり、新しく<T>型の変数(ytで属性はFLAG.DIVIDED_T)が生成されます。
チップ：
生成された<T>型変数の名前は "元の名前#T" となり（"#T"の２文字が元の名前に追加される）、元の変数の右辺変数を全て引き継ぎます。 （元の変数の右辺変数はそのままですが<F>型として扱われるため計算時点で無視されます。）

ループのようでループでない

見かけ上のループ
分割されて発生したループのF-Tが他のF-T型に結びついて、実質ループが解消される場合があります。 上図では下部の A-G を最初に解いてから、上部の F-T を解けば、1次元の方程式を２回解くだけの問題になり、連立させる必要がなくなります。 ただし、図のループの右の変数が分割されると、独立なルート（後述）が無くなるのでエラーとなります（分割したい変数、またはしたくない変数を指定することができます）。
チップ：
USERFLAG.DIVISIBLE を<DD>型にしてほしい変数に、USERFLAG.INDIVISIBLE は<DD>にしてほしくない変数に設定できます。 ただし、他に分割できる変数が無い場合は USERFLAG.INDIVISIBLE のフラグが付いていても分割される場合があります。 発見したループ上に USERFLAG.DIVISIBLE や USERFLAG.INDIVISIBLE のフラグを持つ変数が無い場合、 複数のループに関係している変数（があれば）が優先して、そうでなければ最初に見つかった変数が分割されます。

先頭へ

参照

先頭へ