Mol (Math Object Library) for .Net 例題:アルゴリズム工房

共通例題ツール
BigDecimal
ベクトル
行列
スプライン
高速フーリェ変換
乱数
統計計算
連立方程式
固有値
特異値分解
線形最小二乗問題
非線形最小二乗問題

Mol には Visual Studio (2010) のソリューションファイル付の例題集が用意されています。ここでは、代表的な部分について若干の説明と（C# による数値計算）結果を記載しています。各オブジェクト等の詳細はリファレンスを参照してください。

　共通例題ツール

以下は、各例題で共通に使用されているツールクラス（public static class T）で、結果の出力や計算結果の確認に使用します。
詳細は例題のソースコード(Test.cs)を参照してください。
情報はコンソールに出力（Consoleが有効であること）されます（例題はコンソールアプリケーションとしてビルドされます）。

プロパティ／メソッド	説明
double PI = 3.14159265358979	円周率
int Frac = 3	小数点以下の出力桁数（デフォルトは３）
string Format = "F"+Frac	数値を出力する書式（デフォルトは　"F3"）
int Length = Frac+3	数値出力の全桁数（デフォルトは　Frac+3）
void P(string st)	文字列(st)を出力後、改行します
void P(string title, _Matrix m)	行列(m)を出力
void P(string title, _Vector v)	ベクトル(v)を出力
void W(string st)	st をコンソールに出力（改行無）
void WL(string st)	st をコンソールに出力（改行有）
string R(string st)	文字列を右詰めに(前にスペースを付けてから後ろからLength個の文字をリターン)する
void Assert(bool f)	f が true か確認します。true なら何もしません。false ならメッセージボックスを表示します
void Assert(bool f, string st)	f が true か確認します。true なら何もしません。false ならタイトル文字のメッセージボックスを表示します
void EQ(t1, t2)	t1 と t2 が等しいかチェックします。等しいなら何もしません。等しくなければメッセージボックスを表示します。 t1/t2 は double/Complex/_Vector/_Matrix を指定可

　BigDecimal の例

BigDecimal は可変多倍長の計算をサポートするクラスです。計算桁数はメモリーと時間が許す限り増やすことができます。
基本的に四則演算のうち + - * は桁落ち等の誤差は生じません。
割り算 / は循環小数になり得るので、分子と分母の桁数から結果の桁数が決まります。従って、丸め等による誤差が生じる可能性があります。
いずれにせよ、四則演算 + - * / を使用する限り、計算結果の有効桁数は大きくなるので、どこかで計算を打ち切り、丸める必要があります。
これに対して、Add/Sub/Mul/Div や Sqrt 等のメソッドには結果の桁数を指定することができます。
円周率の計算（マチンの公式による）や Sin/Cos/Log/Exp 等（級数展開）の計算例は BigMath.cs に記述されていますので参照してください。


  BigDecimal b = BigDecimal.Three.Sqrt(100); // 3の平方根を100桁まで計算する。
  T.P("Sqrt(3)    =" + b);
  T.P("Sqrt(3)**2 =" + (b*b));
  T.P("Sqrt(3).LengthRound(20, BigDecimal.ROUND_MODE.DOWN)     =" + b.LengthRound(20, BigDecimal.ROUND_MODE.DOWN));
  T.P("Sqrt(3).LengthRound(20, BigDecimal.ROUND_MODE.UP)       =" + b.LengthRound(20, BigDecimal.ROUND_MODE.UP));
  T.P("Sqrt(3).LengthRound(10, BigDecimal.ROUND_MODE.HALF_UP)  =" + b.LengthRound(10, BigDecimal.ROUND_MODE.HALF_UP));
  T.P("Sqrt(3).LengthRound(10, BigDecimal.ROUND_MODE.HALF_DOWN)=" + b.LengthRound(10, BigDecimal.ROUND_MODE.HALF_DOWN));
  T.P("Sqrt(3).PointRound(10, BigDecimal.ROUND_MODE.CEIL)      =" + b.PointRound(10, BigDecimal.ROUND_MODE.CEIL));
  T.P("Sqrt(3).PointRound(10, BigDecimal.ROUND_MODE.FLOOR)     =" + b.PointRound(10, BigDecimal.ROUND_MODE.FLOOR));
  b = b.LengthRound(30);
  T.P("b.ToString(\"+F,10\")=" + b.ToString("+F,10"));
  T.P("b.ToString(\" F\")   =" + b.ToString(" F"));

結果は以下のようになります。


Sqrt(3)    = 0.1732050807 5688772935 2744634150 5872366942 8052538103 8062805580 ... 576E+1
Sqrt(3)**2 = 0.3000000000 0000000000 0000000000 0000000000 0000000000 0000000000 ... 776E+1
Sqrt(3).LengthRound(20, BigDecimal.ROUND_MODE.DOWN)     = 0.1732050807 5688772935E+1
Sqrt(3).LengthRound(20, BigDecimal.ROUND_MODE.UP)       = 0.1732050807 5688772936E+1
Sqrt(3).LengthRound(10, BigDecimal.ROUND_MODE.HALF_UP)  = 0.1732050808E+1
Sqrt(3).LengthRound(10, BigDecimal.ROUND_MODE.HALF_DOWN)= 0.1732050807E+1
Sqrt(3).PointRound(10, BigDecimal.ROUND_MODE.CEIL)      = 0.1732050807 6E+1
Sqrt(3).PointRound(10, BigDecimal.ROUND_MODE.FLOOR)     = 0.1732050807 5E+1
b.ToString("+F,10")=+1.7320508075,6887729352,744634151
b.ToString(" F")   = 1.73205080756887729352744634151

　ベクトルの例

ベクトルは基本的に一次元配列と同じように扱えますが、先頭配列のインデックスは 1 から開始します。
_Mol.IndexBase を操作して 0 から開始するようにもできます。
ベクトルには行列と同じく密と疎、さらに double と Complex の違いがあります。
またベクトル同士の + - * 、行列との * 、またスカラーとの * / 等の演算が定義されています。


  VectorDenseDouble   vdd = new VectorDenseDouble(5);
  VectorDenseComplex  vdc = new VectorDenseComplex(5);
  VectorSparseDouble  vsd = new VectorSparseDouble(5);
  VectorSparseComplex vsc = new VectorSparseComplex(5);
  vdd[1] = 1; vdd[3] = 3; vdd[5] = 5;
  vsd[1] = 1; vsd[3] = 3; vsd[5] = 5;
  vdc[2] = new Complex(2, 2); vdc[4] = new Complex(4, 4);
  vsc[2] = new Complex(2, 2); vsc[4] = new Complex(4, 4);
  T.P("vdd:", vdd);
  T.P("vdd.Count=" + vdd.Count);
  T.P("vdd.Norm1=" + vdd.Norm1());
  T.P("vdd.Norm2=" + vdd.Norm2());
  T.P("vdd.NormI=" + vdd.NormI());
  T.P("vdc:", vdc);
  T.P("vsd:", vsd);
  T.P("vsc:", vsc);
  T.P("vsc.Conjugate():", vsc.Conjugate());
  T.P("vsc.Count=" + vsc.Count);
  T.P("vsc.Norm1=" + vsc.Norm1());
  T.P("vsc.Norm2=" + vsc.Norm2());
  T.P("vsc.NormI=" + vsc.NormI());
  T.P("vdd+vsd:", vdd + vsd);
  T.P("vsd-vdd:", vsd - vdd);
  T.P("vdc+vsc:", vdc + vsc);
  T.P("vsc-vdc:", vsc - vdc);
  T.P("vsd*vdd:" + (vsd * vdd));
  T.P("vsc*vdc:" + (vsc * vdc) + "=" +(vsc[2]*vdc[2]+vsc[4]*vdc[4]));
  T.P("vsc*vdc.Conjugate():" + (vsc * (VectorDenseComplex)vdc.Conjugate()));
  T.P("vsd*2.0:" , (vsd * 2.0));
  T.P("vdd/2.0:" , (vdd / 2.0));

結果は以下のようになります。


vdd:
  1.000  0.000  3.000  0.000  5.000
vdd.Count=5
vdd.Norm1=9
vdd.Norm2=5.91607978309962
vdd.NormI=5
vdc:
 ( 0.000, 0.000) ( 2.000, 2.000) ( 0.000, 0.000) ( 4.000, 4.000) ( 0.000, 0.000)
vsd:
  1.000  0.000  3.000
vsc:
 ( 0.000, 0.000) ( 2.000, 2.000)
vsc.Conjugate():
 ( 0.000, 0.000) ( 2.000,-2.000)
vsc.Count=2
vsc.Norm1=8.48528137423857
vsc.Norm2=6.32455532033676
vsc.NormI=5.65685424949238
vdd+vsd:
  2.000  0.000  6.000  0.000 10.000
vsd-vdd:
  0.000  0.000  0.000  0.000  0.000
vdc+vsc:
 ( 0.000, 0.000) ( 4.000, 4.000) ( 0.000, 0.000) ( 8.000, 8.000) ( 0.000, 0.000)
vsc-vdc:
 ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
vsd*vdd:35
vsc*vdc:(0, 40)=(0, 40)
vsc*vdc.Conjugate():(40, 0)
vsd*2.0:
  2.000  0.000  6.000
vdd/2.0:
  0.500  0.000  1.500  0.000  2.500

　行列の例

行列は基本的に二次元配列と同じように扱えますが、先頭配列のインデックスは 1 から開始します。
_Mol.IndexBase を操作して 0 から開始するようにもできます。
行列は一般行列や三角行列等の構造、密と疎、double と Complex の違いがありますが、使用方法に違いはありません。
また行列同士の + - * 、ベクトルとの * 、またスカラーとの * / 等の演算が定義されています。


  MatrixDenseGeneralDouble  mdgd = new MatrixDenseGeneralDouble(3, 4);
  MatrixSparseGeneralDouble msgd = new MatrixSparseGeneralDouble(3, 4);
  for (int i = 1; i <= mdgd.RowCount; ++i)
  {
      for (int j = 1; j <= mdgd.ColumnCount; j+=2)
      {
          mdgd[i, j] = i * 10 + j;
          msgd[i, j] = i * 10 + j;
      }
  }
  T.P("mdgd", mdgd);
  T.P("mdgd+msgd", mdgd+msgd);
  T.P("mdgd.Transpose()", mdgd.Transpose());
  T.P("mdgd==msgd: " +_Mol.EQ(mdgd,msgd));
  T.P("mdgd.Count=" + mdgd.Count);
  T.P("msgd.Count=" + msgd.Count);
  T.P("mdgd*2=" , mdgd*2.0);
  T.P("msgd/2=" , msgd/2.0);
  T.P("msgd.Norm1()=" + msgd.Norm1());
  T.P("msgd.NormE()=" + msgd.NormE());
  T.P("msgd.NormI()=" + msgd.NormI());

結果は以下のようになります。


mdgd
 11.000  0.000 13.000  0.000
 21.000  0.000 23.000  0.000
 31.000  0.000 33.000  0.000
mdgd+msgd
 22.000  0.000 26.000  0.000
 42.000  0.000 46.000  0.000
 62.000  0.000 66.000  0.000
mdgd.Transpose()
 11.000 21.000 31.000
  0.000  0.000  0.000
 13.000 23.000 33.000
  0.000  0.000  0.000
mdgd==msgd: True
mdgd.Count=12
msgd.Count=7
mdgd*2=
 22.000  0.000 26.000  0.000
 42.000  0.000 46.000  0.000
 62.000  0.000 66.000  0.000
msgd/2=
  5.500  0.000  6.500  0.000
 10.500  0.000 11.500  0.000
 15.500  0.000 16.500  0.000
msgd.Norm1()=69
msgd.NormE()=57.5325994545701
msgd.NormI()=64

　スプラインの例

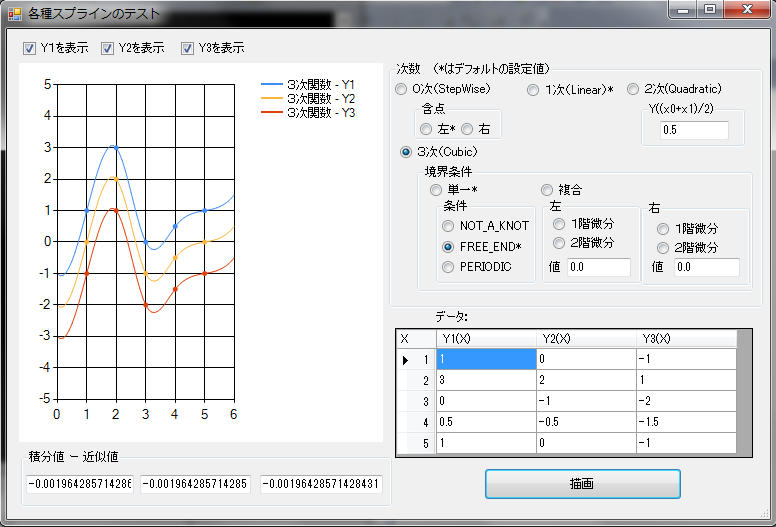
スプライン計算は DataFitting クラスが提供します。
スプラインは数値で与えられた n 個のデータ点列　(x_i, y_i(x_i)) (i=1,2,...,n) 　の n-1 個の区間（x_i < x_i+1） (i=1,2,...,n-1)　を多項式（n-1個）で結びます（各多項式は同じ次数で各項の係数だけが異なるものとします）。

各区間の多項式(P_i(x))は基本的に以下のような形になります（i は区間番号、i=1,2,...,n-1）。

　　P_i(x) = C_i,0 + C_i,1(x - x_i)¹ + ... + C_i,k(x - x_i)^k 　ただし　　x_i ≤ x ≤ x_i+1

ここで C_i,j は i 番目の区間の多項式（P_i(x)）の j 次の項の係数（定数）。 k は多項式の（最大）次数となります( 0 ≤ j ≤ k )。 k（次数）は 0～3 までを選択できます。２次は一つ、３次の場合は二つの境界条件（値）を指定する必要があります（詳細はリファレンスを参照してください。）。

スプラインを利用するにはまず DataFitting オブジェクトを作成してデータ点列と多項式オブジェクト（SplineStepWise：０次、SplineLinear：１次、SplineQuadratic:２次、SplineCubic:３次）の一つを作成してセットします。その後 DataFitting オブジェクトの ComputeAt() や Integrate() メソッドでそれぞれ補間や積分が計算できます。


    int N = 1000;
    int M   10;
    VectorDenseDouble        x = VectorDenseDouble(N);          // X-座標
    MatrixDenseGeneralDouble Y = MatrixDenseGeneralDouble(N,M); // x[i] に対して Y[i,1～M] の値を対応付ける行列(ベクトル可)。
    // .......... x と y に値を設定
    DataFitting df = new DataFitting(x, Y); // DataFitting オブジェクトの作成
    SplineCubic s3 = new SplineCubic();     // ３次スプラインオブジェクトの作成
    s3.SetBoundaryCondition(SplineCubic.SINGLE_BOUNDARY_CONDITION.FREE_END); // FREE_END 境界条件
    df.SetSpline(s3);                       // DataFitting オブジェクトに３次スプラインを設定
    // 補間の実行（キャストは必要、0.5 ではなくベクトルを指定すると戻り値は行列になります）
    VectorDenseDouble y = (VectorDenseDouble)df.ComputeAt(0.5); // x=0.5 のときの y[1],y[2],...,y[M] を計算
    // y は M 個の要素を持つベクトル
    // ......... 処理

例では MSChart コントロールを使用して各次数でデータ点列がどのように結ばれる（補間）か視覚的に確認できるようになっています。各条件を設定したら「描画」ボタンをクリックします。*の付いたものはデフォルトの設定です。多項式が決定するのでスプラインは補間と同時に区間の積分が計算できます。「積分値-近似値」の欄は計算した積分値から各計算区間を台形で近似した値です。当然ながら一次（線形）スプラインの場合は積分値＝近似値となります。

　高速フーリェ変換（FFT）の例

高速フーリェ変換（FFT）計算は DftDouble や DftComplex クラスが提供します。

与えられた N 個の（実験値や測定値の）データ列 Wj (j=0,1,2,...,N-1) について

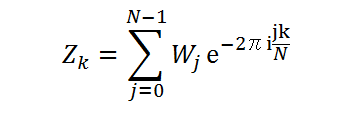という変換を離散フーリェ変換(Forward:前進変換)といいます。また、逆に

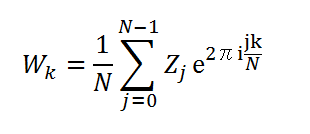と Z から W を計算する場合をフーリェ逆変換(Backward:後退変換)といいます。
ここで、元データ W は実数か複素数です。一方、変換データ Z は全て複素数になります。
W が実数の場合は DftDouble クラス、複素数の場合は DftComplex クラスを使用します。

前記２式は一次元のデータ列ですが、Mol（MKL）では多次元に拡張した以下の一般式を用いて、多次元データ Y と X を相互に高速変換（FFT）します。

ここで i は虚数単位、d（≧1）は次元数（インデックスの数）、N_i（0≦i≦d-1）は各次元サイズ（各インデックスの最大値。 δは変換の方向を決定する因子で前進（Foward）変換の時は -1、後退（Backward）変換の時は +1 が設定されます。Y と X には、上記 W と Z に当たる多次元の配列データを変換方向に応じて設定します。 σはスケール因子でデフォルトで前進変換のときは 1.0、後退（逆）変換の時は 1.0/(N₀・N₁・...N_d-1) が設定（変更可）されます。

例題の TestDFT.cs には上式をそのまま忠実に計算する LasyDFT クラスが記述されています。値と計算時間の確認に利用できます。ただし、例題では LasyDFT に対する呼び出し（TestDFT.ComputeForward()参照）は（遅すぎるため）コメントになっています。値の確認等のためコメントを外すときはデータ点数を（大幅に）減らしてください。

Molでの計算は非常に簡単で、以下の手順になります。

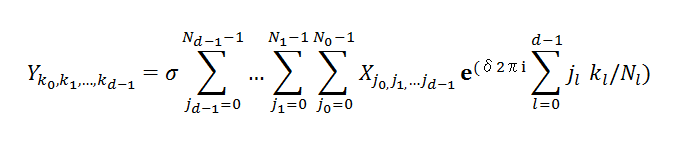
DftDouble(元データが実数の時)、または DftComplex(元データが複素数の時)をデータの数を指定して作成。
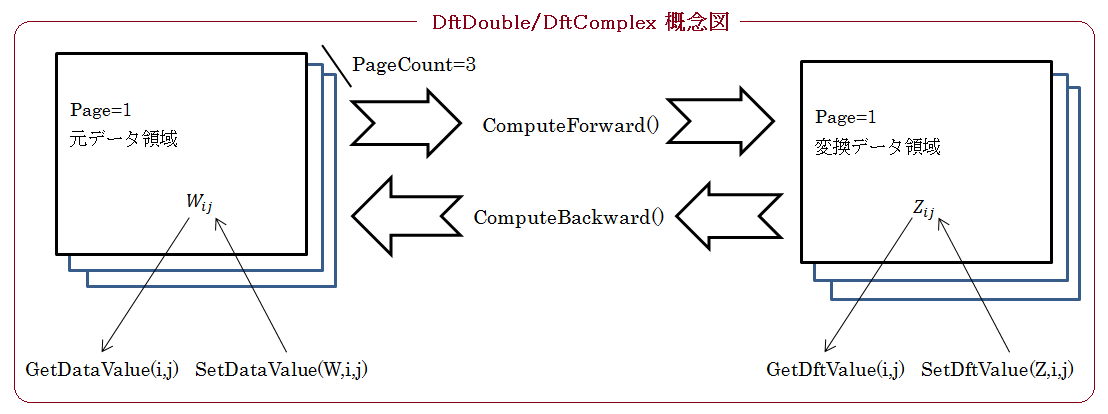
※DftDouble/DftComplexオブジェクトは作成時に「元データ」と「変換データ」の領域を確保・管理します。
※同じサイズのデータが複数ある場合は、データ領域も複数個確保されます（各データ領域は Page（初期値は1）で指定されます）。
```
    int P = 3;     // 同じデータの組が３個ある場合。
    int M = 10000; // 行数
    int N = 1000;  // 列数
    // DftDouble/DftComplexのコンストラクターは可変個（ページ数＋次元サイズ）の引数可
    DftDouble dft = new DftDouble(P,M,N); // 行列 A[M,N] のデータが P 個あるイメージ
```

元データ領域にデータを設定（通常操作）


    for(int p=1;p<=P;++p)
    {
        dft.Page = p;
        for(int i=1;i<=M;++i)
        {
            for(int j=1;j<=N;++j)
            {
                double W = ..... // A[i,j] 要素のデータ取得
                dft.SetDataValue(W,i,j); //　データの設定（ページは p, i と j は FORTRAN 形式）
            }
        }
    }

フーリェ変換の実行（結果は変換データ領域に格納される）。
```
    dft.ComputeForward();
```

計算結果を取得する。


    for(int p=1;p<=P;++p)
    {
        dft.Page = p;
        for(int i=1;i<=M;++i)
        {
            for(int j=1;j<=N;++j)
            {
                Complex Z = dft.GetDftValue(i,j); //　変換データの取得（ページは p, i と j は FORTRAN 形式）
                ...............
            }
        }
    }

※コンストラクター、GetDataValue()、GetDftValue()、SetDataValue()、SetDftValue()等はデータの次元に応じた可変個の引数を受け取ることに注意してください。

　乱数の例

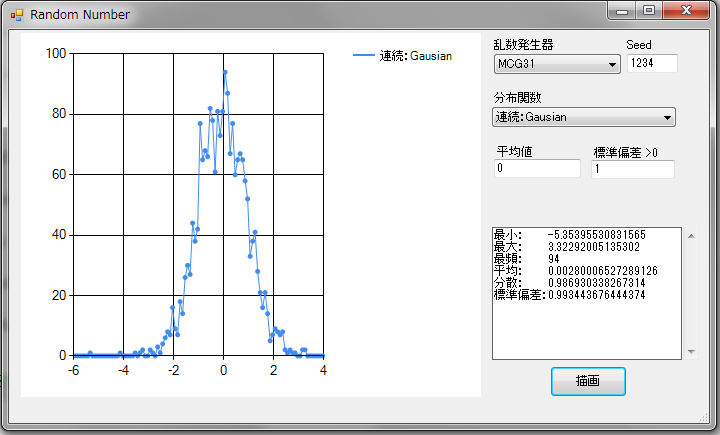
乱数列の生成は RandomNumber クラスが提供します。
乱数、特に確率分布に従った乱数は統計的な計算に有用です。乱数列の生成にはまず RandomNumber オブジェクトを疑似乱数生成器と種（Seed）を指定して作成します。 Seed は任意の整数で乱数を計算する基になります。疑似乱数生成器と Seed が同じ場合、同じ乱数列が毎回生成されます。


    // 疑似乱数発生器は 31 ビット乗算合同生成器、Seed は　1234。
    RandomNumber rnd = new RandomNumber(RandomNumber.GENERATOR.BRNG_GENERATOR.BRNG_MCG31, 1234);

次に、乱数列を格納するベクトルと、各種統計分布に従ったパラメーターを引数にしてメソッドを呼ぶだけです。例えば正規分布なら平均値（例では0）と標準偏差（例では 1.0）を指定して rnd.GenerateGausian() メソッドを呼び出します。
※疑似乱数生成器で生成された乱数は正規分布に従うように変換されますので、変換方法も指定します。


    VectorDenseDouble vals = new VectorDenseDouble(1000);
    // 平均値 0、標準偏差 1.0 の正規分布に従った乱数をボックスミューラー法を指定して 1000 個生成する。
    rnd.GenerateGaussian(vals, 0.0, 1.0, RandomNumber.GAUSSIAN_METHOD.BOXMULLER);

例では MSChart コントロールを使用して生成した乱数を視覚的（度数分布グラフ）に確認できるようになっています。縦軸は最小値と最大値間を１００等分して各区間に入る乱数をカウントしたものです。この時、統計計算クラス(Stat)を使用して乱数列の最小値、最大値、分散・標準偏差を計算して乱数列が指定した統計分布に従っていることを確認できます。

　統計計算の例

各種統計計算は Stat クラスが提供します。
統計計算の例として、生徒の試験点数を考えることにします。学校の全生徒数を N 人、試験科目を P （例えば国語、英語、社会、理科、数学の５科目なら P = 5）とします。各科目毎の最小値、最大値、平均値、相関行列（例えば国語の点数と数学の点数に関連があるかどうか等）を計算するには、以下のように行数 N、列数 P の行列を作成します。 score[i,j] に、i 番目の生徒の j 科目の点数を格納します。


    int N = 1000; // 生徒の数（標本数）
    int P = 5;    // 科目数（次元数）
    MatrixDenseGeneralDouble score = MatrixDenseGeneralDouble(N,P);
    for(int i = 1;i<=N;++i)
    {
        for(int j=1;j<=P;++j)
        {
            ..... 点数の取得 (=v)
            score[i,j] = v;  // score[i,j] に、i 番目の生徒の j 科目の点数(v)を格納します。
        }
    }

次に作成した行列を引数にして Stat オブジェクトを作成します。さらに計算したい統計量が最小値、最大値、平均値、相関行列なら Stat オブジェクトの Computed プロパティにそれぞれのフラグを設定します（平均値は必ず計算されるので指定する必要はありません）。そして、ComputeProperties() メソッドを呼び出すだけです。


    Stat stat = new Stat(score);
    stat.Computed = Stat.PROPERTIES.MIN | Stat.PROPERTIES.MAX | Stat.PROPERTIES.CORRELATION_MATRIX;
    stat.ComputeProperties();
    // 計算結果は以下のように、stat の各プロパティに格納されます。
    /*
      stat.DataMatrix        ... データ行列（scoreへの参照）
      stat.Min               ... 各科目の最小値を格納したベクトル（サイズ P）
      stat.Max               ... 各科目の最大値を格納したベクトル（サイズ P）
      stat.Mean              ... 各科目の平均値を格納したベクトル（サイズ P）
      atat.CorrelationMatrix ... 各科目間の相関行列（サイズ P x P）
    */

stat.Min や stat.Max の初期値は null です。 stat.ComputeProperties() メソッドは計算開始前に Computed プロパティに設定されているフラグをチェックします。そして、対応する Max や Min 等が null ならば自動的にベクトルや行列を作成してセットします。Computed フラグを使用しなくても、自分でベクトルや行列を作成して stat の各種プロパティに設定することも可能です。この場合、一旦、設定しても後で null を設定すれば設定した統計量は計算から除外されます。

Statオブジェクトの各プロパティ（ベクトルや行列）のイメージ図は以下のようになります（詳細はリファレンスを参照してください）。
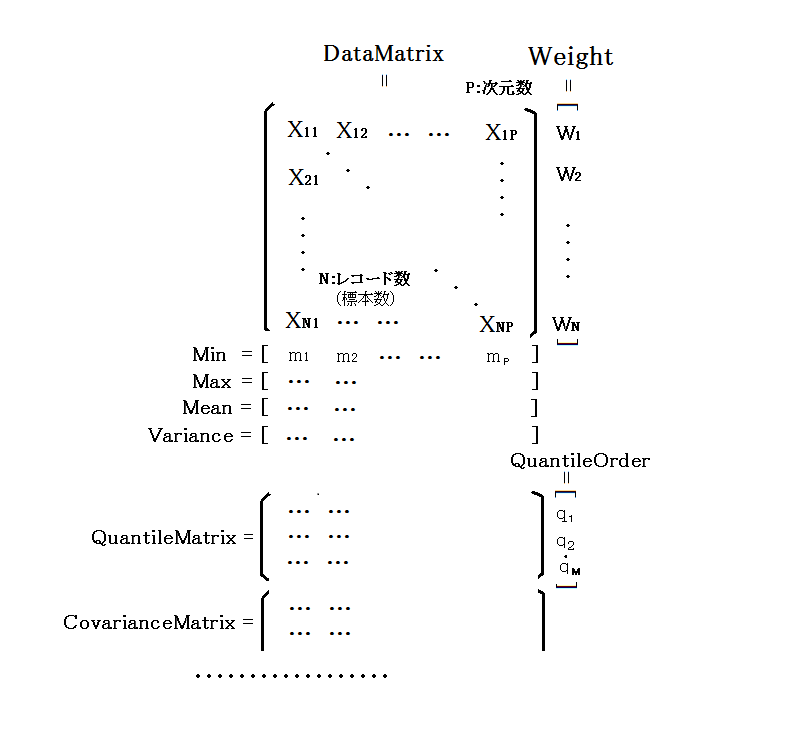
以上は「一括計算」の例です。上記の計算を全国の全生徒に対して実行する場合、DataMatrix に全ての点数データを保持するにはサイズ（N）が大きすぎてメモリーが不足する可能性があります。このような巨大なデータを扱う場合でも、 DataMatrix には一つの学校分のデータを格納して繰り返し全学校分のデータを処理（DataMatrixにコピー後 ComputeProperties メソッドを呼び出す）することができます。DataMatrix は使い回しできます。または、別途作成した行列（行数は変更できますが列数を変更することはできません）を DataMatrix に都度セットしてもかまいません。このような処理を「分割処理」と呼びます。分割処理を実行する場合、最初は stat.ComputeProperties(0) と必ず ComputeProperties の引数にゼロを指定します。その後はゼロ以外の引数を指定してください。

サンプルプログラム TestStat.cs ではまず大きな stat1.DataMatrix で各種統計量を一括計算してから別の Stat オブジェクト（stat2）を作成し、stat2.DataMatrix に stat1.DataMatrix の部分行列をコピーしながら分割計算して最終結果を比較しています。

Stat は一つの DataMatrix のみを対象にして

欠測値の置き換え（ReplaceMissingValues）
外れ値の検出（DetectOutliers）
外れ値を考慮した統計量（ComputeRobustStat）
部分分散行列・部分相関行列（ComputePartialCovarianceCorrelationMatrix）
グループ分けと配分した平均値や分散行列（ComputePooledGroupEstimates）
相関行列の半正定値化（ParameterizeCorrelationMatrix）

等の計算がサポートされていますので、それらのテストコードも含まれています。

※
欠測値は MissingValue を DataMatrix の要素にセットします。 MissingValue の値は非数値（Double.NaN）です。 NaN は算術比較に用いることはできません。自分自身も含めて、全てに一致しません（NaN!=NaNです）。従って、数値がNaNであるかどうかは IsMissingValue()メソッドを使用してください。

　連立方程式

LuSolver クラスは A*x = b の連立方程式を解きます。
ここで、 A は正則の正方行列^注）、b はベクトル、または行列。解 x は b がベクトルならベクトル、行列なら行列。
最初に LuSolver lu = LuSolver.Create(A) と A を因子分解します。因子分解の結果を用いて X = lu.Solve(b) のように解を求めます。
一度の因子分解で、異なる b による解を何度も解くことができます。
b が行列の時はマルチCPU、マルチスレッドの恩恵を受けることができます。
例の行列宣言部分を変更しても答えは変わらないことを確認してください（計算時間とメモリー使用量は異なります）。

注）

行列 A は Mol で定義されている全てのタイプを指定できます。もちろん、A のタイプに応じて最適な解法が自動的に選択されます（ので利用者は特に気にする必要はありません）。特に A が疎（スパース）である時は有名な PARDISO が使用されます。
もっと大規模な例題は行列データとベンチマークの項を参照してください。


//  MatrixDenseGeneralDouble A = new MatrixDenseGeneralDouble(4, 4);
//  A.UserType = _Mol.USER_TYPE.USER_MATRIX_SYMMETRIC; // 一般行列上に対称行列を作成
// MatrixDenseSymmetricDouble A = new MatrixDenseSymmetricDouble(4);
   MatrixSparseSymmetricDouble A = new MatrixSparseSymmetricDouble(4);
   A[1, 1] = 1; A[1, 2] = -2; A[1, 3] = 3; A[1, 4] = 1;
   A[2, 2] = 1; A[2, 3] = -2; A[2, 4] = -1;
   A[3, 3] = 1; A[3, 4] = 5;
   A[4, 4] = 3;
   // 下半分も設定する（対称行列では不必要）。
   //for (int i = 1; i <= A.RowCount; ++i)
   //{
   //    for (int j = 1; j < i; ++j) A[i, j] = A[j, i];
   //}
   MatrixDenseGeneralDouble B = new MatrixDenseGeneralDouble(4, 2);
   B[1, 1] =  3; B[1, 2] = 1;
   B[2, 1] = -4; B[2, 2] = 1;
   B[3, 1] =  7; B[3, 2] = 1;
   B[4, 1] =  8; B[3, 2] = 1;
   LuSolver lu = LuSolver.Create(A);
   MatrixDenseGeneralDouble X = lu.Solve(B);
   T.P("係数行列 A=", A);
   T.P("B=", B);
   T.P("X=", X);
   T.P("(A*X-B)=", A * X - B);

結果は以下のようになります。


係数行列 A=
  1.000 -2.000  3.000  1.000
 -2.000  1.000 -2.000 -1.000
  3.000 -2.000  1.000  5.000
  1.000 -1.000  5.000  3.000
B=
  3.000  1.000
 -4.000  1.000
  7.000  1.000
  8.000  0.000
X=
  1.000 -1.038
  1.000 -1.231
  1.000 -0.269
  1.000  0.385
(A*X-B)=
  0.000  0.000
  0.000  0.000
  0.000  0.000
  0.000  0.000

　固有値問題

固有値計算は EgvSolver クラスが提供します。
固有値問題解法とは、行列 A が与えられたときに、以下の式を満たす固有値 λ と、対応する固有ベクトル x を計算します。

Ax_i = λ_ix_i : 標準固有値問題
Ax_i = λ_iBx_i: 汎用固有値問題 (A と B は同じタイプの行列で、かつ、B は正定値である必要があります)。

λ と x は A の列（行）の数だけあります。
従って、固有値λ はベクトル、固有ベクトル x は行列（列 i が x_i に対応します）の形で計算されます。
A が実数対称行列、またはエルミート行列の場合、λ は実数（Aが複素数なら虚数部がゼロの複素数）になります。
x は A が複素数なら複素数一般行列になります。

固有値問題の解法は全てスタティックメソッドで実行され、引数に渡される行列やベクトルは内容が書き換えられます。
従って例のように必要なら Clone() メソッドで同じ行列を作成してください。

※行列(Aとします)は A.Columns[i] や A.Rows[i] という形で、それぞれ i 番目の列ベクトル、行ベクトルを取り出すことができます。
※もっと大規模な例題は行列データとベンチマークの項を参照してください。）


 {
     MatrixDenseSymmetricDouble S = new MatrixDenseSymmetricDouble(5);
     S[1, 1] = 6.29; S[1, 2] = -0.39; S[1, 3] = 0.61; S[1, 4] = 1.18; S[1, 5] = -0.08;
     S[2, 2] = 7.19; S[2, 3] = 0.81; S[2, 4] = 1.19; S[2, 5] = -0.08;
     S[3, 3] = 5.48; S[3, 4] = -3.13; S[3, 5] = 0.22;
     S[4, 4] = 3.79; S[4, 5] = -0.26;
     S[5, 5] = 0.83;

     MatrixDenseGeneralDouble A = new MatrixDenseGeneralDouble(5, 5);
     for (int i = 1; i <= 5; ++i)
     {
         for (int j = 1; j <= 5; ++j) A[i, j] = S[i, j];
     }

     VectorDenseDouble eigen_values = new VectorDenseDouble(5);
     MatrixDenseGeneralDouble eigen_vectors = new MatrixDenseGeneralDouble(5, 5);

     T.P("General A:", A);
     EgvSolver egv = EgvSolver.Solve(eigen_values, eigen_vectors,
                                     (MatrixDenseGeneralDouble)A.Clone());
     T.P("eigen_values:", eigen_values);
     T.P("eigen_vectors:", eigen_vectors);
     for (int i = 1; i <= 5; ++i)
     {
         T.P("A*eigen_vectors[" + i + "] - eigen_values[" + i + "]*eigen_vectors[" + i + "]",
              A * eigen_vectors.Columns[i] - eigen_values[i] * eigen_vectors.Columns[i]);
     }

     T.P("Symmetric S:", S);
     egv = EgvSolver.Solve(eigen_values, eigen_vectors, (MatrixDenseSymmetricDouble)S.Clone());
     T.P("eigen_values:", eigen_values);
     T.P("eigen_vectors:", eigen_vectors);
     for (int i = 1; i <= 5; ++i)
     {
         T.P("S*eigen_vectors[" + i + "] - eigen_values[" + i + "]*eigen_vectors[" + i + "]",
              S * eigen_vectors.Columns[i] - eigen_values[i] * eigen_vectors.Columns[i]);
     }
 }
 { // 汎用問題（Bは正定値）
     MatrixDenseHermite A = new MatrixDenseHermite(4);
     A[1, 1] = new Complex(3, 0);
     A[1, 2] = new Complex(0, 2);
     A[1, 3] = new Complex(1, 1);
     A[1, 4] = new Complex(0, 1);
     A[2, 2] = new Complex(3, 0);
     A[2, 3] = new Complex(0, 2);
     A[2, 4] = new Complex(1, 1);
     A[3, 3] = new Complex(3, 0);
     A[3, 4] = new Complex(0, 2);
     A[4, 4] = new Complex(3, 0);

     MatrixDenseHermite B = new MatrixDenseHermite(4);
     B[1, 1] = new Complex(2, 0); B[1, 2] = new Complex(1, 1); B[1, 3] = new Complex(0, 1);
     B[2, 2] = new Complex(2, 0); B[2, 3] = new Complex(1, 1); B[2, 4] = new Complex(0, 1);
     B[3, 3] = new Complex(2, 0); B[3, 4] = new Complex(1, 1);
     B[4, 4] = new Complex(2, 0);

     VectorDenseComplex eigen_values = new VectorDenseComplex(4);
     MatrixDenseGeneralComplex eigen_vectors = new MatrixDenseGeneralComplex(4, 4);
     T.P("A:", A);
     T.P("B:", B);
     EgvSolver egv = EgvSolver.Solve2(eigen_values, eigen_vectors, (MatrixDenseHermite)A.Clone(), 
                                       (MatrixDenseHermite)B.Clone());
     T.P("eigen_values:", eigen_values);
     T.P("eigen_vectors:", eigen_vectors);
     for (int j = 1; j <= 4; ++j)
     {
       T.P("A * eigen_vectors.Columns[" + j + "] - eigen_values[" + j + "]*B*eigen_vectors.Columns[" + j + "] =",
            A * eigen_vectors.Columns[j] - eigen_values[j] * B * eigen_vectors.Columns[j]);
     }
 }

結果は以下のようになります。


General A:
  6.290 -0.390  0.610  1.180 -0.080
 -0.390  7.190  0.810  1.190 -0.080
  0.610  0.810  5.480 -3.130  0.220
  1.180  1.190 -3.130  3.790 -0.260
 -0.080 -0.080  0.220 -0.260  0.830
eigen_values:
  0.710  0.824  6.577  7.525  7.944
eigen_vectors:
  0.221  0.090 -0.951  0.119  0.155
  0.208  0.085 -0.039 -0.962  0.153
 -0.525 -0.215 -0.291 -0.237 -0.733
 -0.726 -0.215 -0.093 -0.070  0.643
 -0.324  0.945  0.007  0.005 -0.050
A*eigen_vectors[1] - eigen_values[1]*eigen_vectors[1]
  0.000  0.000  0.000  0.000  0.000
A*eigen_vectors[2] - eigen_values[2]*eigen_vectors[2]
  0.000  0.000  0.000  0.000  0.000
A*eigen_vectors[3] - eigen_values[3]*eigen_vectors[3]
  0.000  0.000  0.000  0.000  0.000
A*eigen_vectors[4] - eigen_values[4]*eigen_vectors[4]
  0.000  0.000  0.000  0.000  0.000
A*eigen_vectors[5] - eigen_values[5]*eigen_vectors[5]
  0.000  0.000  0.000  0.000  0.000
Symmetric S:
  6.290 -0.390  0.610  1.180 -0.080
 -0.390  7.190  0.810  1.190 -0.080
  0.610  0.810  5.480 -3.130  0.220
  1.180  1.190 -3.130  3.790 -0.260
 -0.080 -0.080  0.220 -0.260  0.830
eigen_values:
  0.710  0.824  6.577  7.525  7.944
eigen_vectors:
  0.221  0.090 -0.951  0.119  0.155
  0.208  0.085 -0.039 -0.962  0.153
 -0.525 -0.215 -0.291 -0.237 -0.733
 -0.726 -0.215 -0.093 -0.070  0.643
 -0.324  0.945  0.007  0.005 -0.050
S*eigen_vectors[1] - eigen_values[1]*eigen_vectors[1]
  0.000  0.000  0.000  0.000  0.000
S*eigen_vectors[2] - eigen_values[2]*eigen_vectors[2]
  0.000  0.000  0.000  0.000  0.000
S*eigen_vectors[3] - eigen_values[3]*eigen_vectors[3]
  0.000  0.000  0.000  0.000  0.000
S*eigen_vectors[4] - eigen_values[4]*eigen_vectors[4]
  0.000  0.000  0.000  0.000  0.000
S*eigen_vectors[5] - eigen_values[5]*eigen_vectors[5]
  0.000  0.000  0.000  0.000  0.000

A:
 ( 3.000, 0.000) ( 0.000, 2.000) ( 1.000, 1.000) ( 0.000, 1.000)
 ( 0.000,-2.000) ( 3.000, 0.000) ( 0.000, 2.000) ( 1.000, 1.000)
 ( 1.000,-1.000) ( 0.000,-2.000) ( 3.000, 0.000) ( 0.000, 2.000)
 ( 0.000,-1.000) ( 1.000,-1.000) ( 0.000,-2.000) ( 3.000, 0.000)
B:
 ( 2.000, 0.000) ( 1.000, 1.000) ( 0.000, 1.000) ( 0.000, 0.000)
 ( 1.000,-1.000) ( 2.000, 0.000) ( 1.000, 1.000) ( 0.000, 1.000)
 ( 0.000,-1.000) ( 1.000,-1.000) ( 2.000, 0.000) ( 1.000, 1.000)
 ( 0.000, 0.000) ( 0.000,-1.000) ( 1.000,-1.000) ( 2.000, 0.000)
eigen_values:
 (-3.236, 0.000) ( 1.218, 0.000) ( 1.236, 0.000) (14.782, 0.000)
eigen_vectors:
 (-0.427, 0.625) (-0.235, 0.361) (-0.348,-0.074) (-0.854, 0.621)
 (-0.839,-0.493) ( 0.176,-0.163) (-0.100,-0.207) ( 0.640,-0.730)
 ( 0.066,-0.971) ( 0.233,-0.059) (-0.141, 0.182) (-0.947,-0.213)
 ( 0.757, 0.000) (-0.431, 0.000) (-0.356, 0.000) ( 1.056, 0.000)
A*eigen_vectors.Columns[1] - eigen_values[1]*B*eigen_vectors.Columns[1] =
 ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
A*eigen_vectors.Columns[2] - eigen_values[2]*B*eigen_vectors.Columns[2] =
 ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
A*eigen_vectors.Columns[3] - eigen_values[3]*B*eigen_vectors.Columns[3] =
 ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
A*eigen_vectors.Columns[4] - eigen_values[4]*B*eigen_vectors.Columns[4] =
 ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)

　特異値分解

特異値分解は SvdSolver クラスが提供します。
A を (m × n) の一般行列として、A の特異値分解 (SVD) とは A = UΣV^H の形に分解することです（V^Hは行列 V の複素共役転置）。
ここで、U (m × m) と V (n × n) は、ユニタリ行列 (A が複素行列の場合) または直交行列 (Aが実行列の場合)です。
Σ は、次に示す対角成分σ_i を持つ m × n の対角行列（対角要素のみの帯行列で代用します）になります。

σ₁ ≥ σ₂ ≥ ... ≥ σ_{min(m, n)} ≥ 0

※ σ_i は A の特異値。また、非ゼロの特異値の個数は A の階数(Rank)となります。
※ σ_i は実数です。ただし A が複素数行列の時は Σ も全ての要素の虚数部がゼロの複素数対角（帯）行列となります。

A の条件数（Condition number）は最大特異値 / 最小特異値で表現可能です。
行列 U と V の先頭から min(m, n) の列は、それぞれ、A の左特異ベクトルと右特異ベクトルとなります。
対応する特異値と特異ベクトルは、Av_i = σ_iu_i かつ A^Hu_i = σ_iv_i を満たします。
ここで u_i と v_i は、それぞれ、U と V の i 番目の成分です。

※計算では V ではなく V^H（V の複素共役転置）が得られることに注意してください。
従って、 Av_i = σ_iu_i を計算する場合は、計算結果の複素共役転置を実行して本来の V に戻すことが必要です。
Av の v は計算結果 V の複素共役転置後の列ベクトルです。

※引数の行列やベクトルは上書きされるので、必要なら Clone() メソッド等を使用してください。


 {
     MatrixDenseGeneralDouble A = new MatrixDenseGeneralDouble(3, 3);
     A[1, 1] = 7; A[1, 2] = 2;
     A[2, 1] = 2; A[2, 2] = 6; A[2, 3] = -2;
     A[3, 2] = -2; A[3, 3] = 5;

     MatrixDenseGeneralDouble U = new Mol.MatrixDenseGeneralDouble(3, 3);
     MatrixDenseGeneralDouble V = new Mol.MatrixDenseGeneralDouble(3, 3);
     MatrixDenseBandDouble s = SvdSolver.Solve((MatrixDenseGeneralDouble)A.Clone(), null, U, V);
     // s[1] = 9; s[2] = 6; s[3] = 3;
     T.P("A", A);
     T.P("U", U);
     T.P("s", s);
     T.P("V", V);
     T.P("(A, U * s * V).NormE()=" + (A - U * s * V).NormE());

     MatrixDenseGeneralDouble VT = V.Transpose();
     MatrixDenseGeneralDouble UT = U.Transpose();

     T.P("U*UT", U * U.Transpose());
     T.P("V*VT", V * V.Transpose());
     // 以下は同じこと…
     for (int i = 1; i <= 3; ++i)
     {
         T.P("A * VT.Columns[" + i + "] - s[" + i + "," + i + "] * U.Columns[" + i + "]:",
              A * VT.Columns[i] - s[i, i] * U.Columns[i]);
     }
     for (int i = 1; i <= 3; ++i)
     {
         T.P("UT.Rows[" + i + "] * A - s[" + i + "," + i + "] * V.Rows[" + i + "]:",
              UT.Rows[i] * A - s[i, i] * V.Rows[i]);
     }
 }
 {
     MatrixDenseGeneralComplex A = new MatrixDenseGeneralComplex(3, 4);
     A[1, 1] = new Complex(-5.40, 7.40);
     A[1, 2] = new Complex(6.00, 6.38);
     A[1, 3] = new Complex(9.91, 0.16);
     A[1, 4] = new Complex(-5.28, -4.16);
     A[2, 1] = new Complex(1.09, 1.55);
     A[2, 2] = new Complex(2.60, 0.07);
     A[2, 3] = new Complex(3.98, -5.26);
     A[2, 4] = new Complex(2.03, 1.11);
     A[3, 1] = new Complex(9.88, 1.91);
     A[3, 2] = new Complex(4.92, 6.31);
     A[3, 3] = new Complex(-2.11, 7.39);
     A[3, 4] = new Complex(-9.81, -8.98);

     T.P("A:", A);
     MatrixDenseGeneralComplex U = new Mol.MatrixDenseGeneralComplex(3, 3);
     MatrixDenseGeneralComplex V = new Mol.MatrixDenseGeneralComplex(4, 4);
     MatrixDenseBandComplex s = SvdSolver.Solve2((MatrixDenseGeneralComplex)A.Clone(), null, U, V);
     T.P("U:", U);
     T.P("s:", s);
     T.P("V(Conjugate transposed):", V);
     T.P("(A, U * s * V).NormE()=" + (A - U * s * V).NormE());

     MatrixDenseGeneralComplex VT = V.TransposeConjugate();
     MatrixDenseGeneralComplex UT = U.TransposeConjugate();

     T.P("U*U.TransposeConjugate()", U * UT);
     T.P("V*V.TransposeConjugate()", VT * V);
     // 以下は同じこと…
     for (int i = 1; i <= 3; ++i)
     {
         T.P("A * VT.Columns["+i+"] - s["+i+","+ i+"] * U.Columns["+i+"]:",
              A * VT.Columns[i] - s[i, i] * U.Columns[i]);
     }
     for (int i = 1; i <= 3; ++i)
     {
         T.P("UT.Rows["+i+"] * A - s[" + i + "," + i + "] * V.Rows[" + i + "]:",
              UT.Rows[i]*A  - s[i, i] * V.Rows[i]);
     }
 }

結果は以下のようになります。


A
  7.000  2.000  0.000
  2.000  6.000 -2.000
  0.000 -2.000  5.000
U
 -0.667  0.667 -0.333
 -0.667 -0.333  0.667
  0.333  0.667  0.667
s
  9.000  0.000  0.000
  0.000  6.000  0.000
  0.000  0.000  3.000
V
 -0.667 -0.667  0.333
  0.667 -0.333  0.667
 -0.333  0.667  0.667
(A, U * s * V).NormE()=6.04536571471836E-15
U*UT
  1.000  0.000  0.000
  0.000  1.000  0.000
  0.000  0.000  1.000
V*VT
  1.000  0.000  0.000
  0.000  1.000  0.000
  0.000  0.000  1.000
A * VT.Columns[1] - s[1,1] * U.Columns[1]:
  0.000  0.000  0.000
A * VT.Columns[2] - s[2,2] * U.Columns[2]:
  0.000  0.000  0.000
A * VT.Columns[3] - s[3,3] * U.Columns[3]:
  0.000  0.000  0.000
UT.Rows[1] * A - s[1,1] * V.Rows[1]:
  0.000  0.000  0.000
UT.Rows[2] * A - s[2,2] * V.Rows[2]:
  0.000  0.000  0.000
UT.Rows[3] * A - s[3,3] * V.Rows[3]:
  0.000  0.000  0.000
A:
 (-5.400, 7.400) ( 6.000, 6.380) ( 9.910, 0.160) (-5.280,-4.160)
 ( 1.090, 1.550) ( 2.600, 0.070) ( 3.980,-5.260) ( 2.030, 1.110)
 ( 9.880, 1.910) ( 4.920, 6.310) (-2.110, 7.390) (-9.810,-8.980)
U:
 ( 0.547, 0.000) ( 0.763, 0.000) (-0.344, 0.000)
 (-0.035,-0.151) ( 0.271,-0.226) ( 0.546,-0.744)
 ( 0.813, 0.123) (-0.523,-0.140) ( 0.134,-0.114)
s:
 (21.755, 0.000) ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
 ( 0.000, 0.000) (16.595, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
 ( 0.000, 0.000) ( 0.000, 0.000) ( 3.973, 0.000) ( 0.000, 0.000)
V(Conjugate transposed):
 ( 0.232, 0.207) ( 0.366, 0.386) ( 0.243, 0.328) (-0.561,-0.372)
 (-0.579, 0.403) ( 0.109, 0.172) ( 0.597,-0.275) ( 0.160, 0.055)
 ( 0.604, 0.123) (-0.190, 0.297) ( 0.392, 0.197) ( 0.455, 0.310)
 (-0.083, 0.136) ( 0.696,-0.257) (-0.154, 0.431) ( 0.463, 0.023)
(A, U * s * V).NormE()=3.30357699978985E-14
U*U.TransposeConjugate()
 ( 1.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
 ( 0.000, 0.000) ( 1.000, 0.000) ( 0.000, 0.000)
 ( 0.000, 0.000) ( 0.000, 0.000) ( 1.000, 0.000)
V*V.TransposeConjugate()
 ( 1.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
 ( 0.000, 0.000) ( 1.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
 ( 0.000, 0.000) ( 0.000, 0.000) ( 1.000, 0.000) ( 0.000, 0.000)
 ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000) ( 1.000, 0.000)
A * VT.Columns[1] - s[1,1] * U.Columns[1]:
 ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
A * VT.Columns[2] - s[2,2] * U.Columns[2]:
 ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
A * VT.Columns[3] - s[3,3] * U.Columns[3]:
 ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
UT.Rows[1] * A - s[1,1] * V.Rows[1]:
 ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
UT.Rows[2] * A - s[2,2] * V.Rows[2]:
 ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)
UT.Rows[3] * A - s[3,3] * V.Rows[3]:
 ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000) ( 0.000, 0.000)

　線形最小二乗問題

線形最小二乗問題の計算は LlsSolver クラスが提供します。
線形最小二乗問題(LLS)とは、行列 A(サイズ：m x n) とベクトル b が与えられたときに、二乗和Σ_i((Ax)[i] - b[i])² を最小にするベクトル x を見つけることです。
m ≥ n で rank(A) = n ならば、優決定の連立 1 次方程式 ( 未知数より方程式の個数の方が多い) に対して最小二乗解を計算します

m < n で rank(A) = m の場合は、Ax = b を満たす ( つまり、ノルム||Ax − b||² が最小になる) 解 x は無限に存在します。
これは、劣決定の連立 1 次方程式 (方程式より未知数の個数の方が多い)に対して最小ノルム解（||x||² を最小にする x ）を見つけることになります。

Rank = min(m,n) の場合は最大階数ですが、一般には、A の階数が不明 rank(A) < min(m, n) であり、階数不足の最小二乗問題になります。
この場合は ||x||² も ||Ax − b||² も最小にする最小ノルム・最小二乗解を見つけます。

２番目の例（SolveLSE()）は、以下のような均衡制約を持つ線形最小二乗 (LSE) 問題を解きます。

　　minimize || c - A x ||² ただし、B x = d

A は m × n の行列、B は p × n の行列、c は与えられたm- ベクトル、d は与えられたp- ベクトル。
さらに、p ≤ n ≤ m+p、で Rrank(B) = p、rank(A｜B) = n を仮定します（A｜B は A と B を上下に並べた行列とします）。

※引数の行列やベクトルは上書きされるので、必要なら Clone() メソッド等を使用してください。


 {
     MatrixDenseGeneralDouble A = new Mol.MatrixDenseGeneralDouble(4, 3);
     MatrixDenseGeneralDouble B = new Mol.MatrixDenseGeneralDouble(4, 1);
     VectorDenseDouble b = new Mol.VectorDenseDouble(4);

     double a = 8;
     A[1, 1] = a; A[1, 2] = a; A[1, 3] = a;
     A[2, 1] = a; A[2, 2] = a; A[2, 3] = a;
     A[3, 2] = 1; A[4, 3] = 1;  // answer x = [1/a-2,1,1]

     b[1] = 1; b[2] = 1; b[3] = 1; b[4] = 1;
     T.P("Min|b-Ax|  A:", A);
     T.P("b:", b);

     LlsSolver lls = LlsSolver.SolveKnownRank(A, b);
     T.P("b[1]=" + b[1] + " ==(1.0 / a - 2):" + ((1.0 / a - 2)) );
     T.P("b[2]=" + b[2] + " ==(1.0)");
     T.P("b[3]=" + b[3] + " ==(1.0)");
 }
 { // LSE
     VectorDenseDouble c = new VectorDenseDouble(3);
     VectorDenseDouble x = new VectorDenseDouble(4);
     VectorDenseDouble d = new VectorDenseDouble(3);
     for (int i = 1; i <= c.Size; ++i) c[i] = 1;
     for (int i = 1; i <= d.Size; ++i) d[i] = 1;
     MatrixDenseGeneralDouble A = new MatrixDenseGeneralDouble(3, 4);
     A[1, 1] = 7; A[1, 2] = 2;
     A[2, 1] = 2; A[2, 2] = 6; A[2, 3] = -2;
     A[3, 2] = -2; A[3, 3] = 5;
     MatrixDenseGeneralDouble B = new MatrixDenseGeneralDouble(3, 4);
     B[1, 1] = 2; B[1, 2] = 1;
     B[2, 1] = 1; B[2, 2] = 2; B[2, 3] = 1;
     B[3, 2] = 1; B[3, 3] = 2; B[3, 4] = 1;
     LlsSolver.SolveLSE(x, (MatrixDenseGeneralDouble)A.Clone(), (MatrixDenseGeneralDouble)B.Clone(),
                           (VectorDenseDouble)c.Clone(), (VectorDenseDouble)d.Clone());
     T.P(" Min(|c-Ax|) subject to Bx=d: A", A);
     T.P("      : B", B);
     T.P("      : c", c);
     T.P("      : d", d);
     T.P("(B * x - d).NormE() = " + (B * x - d).NormE());
     T.P("(A * x - c).NormE() = " + (A * x - c).NormE());
 }

結果は以下のようになります。


Min|b-Ax|  A:
  8.000  8.000  8.000
  8.000  8.000  8.000
  0.000  1.000  0.000
  0.000  0.000  1.000
           b:
  1.000  1.000  1.000  1.000

b[1]=-1.875 ==(1.0 / a - 2):-1.875
b[2]=1 ==(1.0)
b[3]=1 ==(1.0)

 Min(|c-Ax|) subject to Bx=d: A
  7.000  2.000  0.000  0.000
  2.000  6.000 -2.000  0.000
  0.000 -2.000  5.000  0.000
                            : B
  2.000  1.000  0.000  0.000
  1.000  2.000  1.000  0.000
  0.000  1.000  2.000  1.000
                            : c
  1.000  1.000  1.000
                            : d
  1.000  1.000  1.000
(B * x - d).NormE() = 2.22044604925031E-16
(A * x - c).NormE() = 2.27607363283981

　非線形最小二乗問題

非線形最小二乗問題の計算は NonlinearEquations クラスが提供します。
非線形最小二乗問題とは、与えられた非線形連立方程式（目的関数）

F_i(X₁,X₂,...,X_n) i=1,2,...,m

の二乗和

S = Σ_i(F_i(X))²

を最小にするベクトル X を見つけることです（実際には二乗和の平方根、S^1/2、ユークリッドノルムを最小にする X を求めます）。
ここで

n は独立変数 X の数
m は式 F の数(連立方程式の元数)

とします(n=m で S=0 なら非線形連立方定式の解を求めることになります)。

まず、この問題を解く手法として

信頼領域法（Trust region 法、m ≥ n である必要があります）
単純探索法

の二つが用意されています。どちらも、解 X の存在範囲（X の上限・下限）を境界条件として与えることができます。

信頼領域法は非常に高速ですが、ヤコビアン行列（∂F_i/∂X_j：行 i=1,2,...,m 列 j=1,2,...,n）の領域を与えること、m ≥ n である必要があります。

単純探索法は X を関数ベクトルの二乗和を減らす方向に単純変化させるもので、低速です。m ≥ n の条件が満たされていれば、なるべく信頼領域法を使用してください（単純探索法はヤコビアン行列は使用せず、上限や下限の一方だけを指定することや m < n でも可能です）。

次に、解き方ですが、まず、連立方程式 F(X) を計算する関数（メソッド）を NonlinearEquations オブジェクトに提供する必要があります。
F(X)は

.Net プログラム（C#等の）で記述し、デリゲート(delegate)として提供
C/C++ 等で記述し、ネイティブな DLL に実装して提供（ネイティブ DLL のロード等は NativeDll クラスを利用します）

の２通りの方法があります。どちらも、NonlinearEquations オブジェクトが呼び出すので、決まった呼出しインターフェースに従う必要があります。当然ながら、どちらも結果は同じです。ネイティブな DLL に実装する方が高速ではありますが、どの程度差が出るかは問題に依存します。

ここでは、ロジスティック曲線のパラメータ推定（カーブ・フィッティング）問題を両方の実装方法で例示します。

※人口、車や家電の普及台数等、最初は緩やかに増加、その後増加速度が速くなり、最後は頭打ちになるような曲線は、動物の成長（たとえば身長とか体重）の過程とも似ているので、成長曲線と呼びます。以下のロジスティック曲線は成長曲線の例の一つです。
y = a/(1+b・exp(-c・x))　......　(1)

パラメータ推定とは、 x と y のペアが、観測や実験の結果として得られ、(x_i,y_i) i=1,2,...,m の点列が上記 (1) を満たす（実際には曲線に近づく）ようにパラメータ a, b, c を決定するものです(F(a,b,c)=y_i - a/(1+b・exp(-c・x_i)))。
実際に求めるものは a,b,c で、それぞれ X[1],X[2],X[3] に対応させます。関数値と測定値の残差は

F_i(X) = y_i - X[1]/(1+X[2]・exp(-X[3]・x_i)) i=1,2,...,m

で、残差二乗和を最小化させる目的関数

S = Σ_i(F_i(X))²

となります。本例では、敢えて、点列 (x_i,y_i) はロジスティック曲線上のものを与えます。当然、境界条件無しなら、ユークリッドノルム値はゼロになります。

まず、目的関数 F(X) を C# で記述する方法は以下のようになります。


/// <summary>
/// 非線形連立方程式の関数計算メソッド（delegate 形式、ネイティブ DLL は必要ありません）。
/// 引数の順序や型、そして戻り値などは以下の通りに設定する必要があります。
/// </summary>
/// <param name="eq">本メソッドを呼び出した NonlinearEquations オブジェクト</param>
/// <param name="F">関数値を出力するためのベクトル（出力）</param>
/// <param name="X">関数値を計算するための独立変数ベクトル（入力）</param>
private void Logistic(NonlinearEquations eq, VectorDenseDouble F, VectorDenseDouble X)
{
    VectorDenseComplex pt = eq.TagComplex;
    for (int i = F.LBound; i <= F.UBound; ++i)
    {
       F[i] = pt[i].Imaginary - X[1] / (1.0 + X[2] * Math.Exp(-X[3] * pt[i].Real));
    }
}

メソッド名 Logistic() は任意ですが、引数は固定されています。関数値、F_i(X)、を計算するには X 以外に点列 (x_i,y_i) が必要です。本例では点列は第一引数 NonlinearEquations オブジェクトの TagComplex プロパティで Logistics() メソッドに渡します（Tag、TagComplex、TagDouble、TagInt 等のプロパティはこのような情報交換に用意されていて、Mol がアクセスすることはありません）。TagComplex、TagDouble、TagInt の配列は C/C++ ネイティブ DLL でもアクセス可能です。

Logistics() メソッドを用意して X の初期値などを設定すれば、後は以下のように MinimizeNorm(x, F) メソッドを呼び出すだけです。


NonlinearEquations eq = new NonlinearEquations(Logistic);
eq.MinimizeNorm(x, F);

C/C++でのネイティブ DLL で F(X) の計算式を定義する例は以下のようになります。各連立方程式の計算値は配列 F に格納されます。点列 (x_i,y_i) は NonlinearEquations オブジェクトの TagComplex プロパティを通じて .Net 側から与えられます（”DATA_POINT *pt = (DATA_POINT*)MOL_GET_COMPLEX_ARRAY_PTR(P);”の部分）。ネイティブ DLL の作成等は例題の Visual Studio 用ソリューションファイルを参照してください。


#include "stdafx.h"
#include <math.h>
#include <stdio.h>

//
// NativeDll クラスから呼び出されるネイティブな関数を定義する場合は、以下のヘッダーファイル（Mol.h）を include してください。
// Mol.h には各種宣言や利用方法などが記述されていますので参考にしてください。
//
#include "Mol.h"

//
// MOL_COMPLEX（や .Net の Complex） と同じ構造を持つ構造体
typedef struct _DATA_POINT
{
	double x;
	double y;
} DATA_POINT;

//
// NonlinearEquations クラス用の非線形連立方程式計算の例です。
// 関数名は任意ですが、引数は以下の例と同じで、順序や型を一致させる必要があります。
// また、戻り値も、計算が成功すれば 0、何らかのエラーが生じた場合は負の整数を返すようにします。
//
// Logistic 曲線へのパラメータ推定。
//
// 引数の説明
//    P[] ... NonlinearEquations クラスの TagInt,TagDouble,TagComplex 等のベクトル等の配列領域アドレスを格納しています。
//            内容については Mol.h のマクロ定義を参照してください。
//    nPtr... P[] の配列サイズ
//    F[] ... 目的関数値を格納するための配列（出力） sqrt(ΣF[i]*F[i]) が最小化されます（i=0,1,...,m-1）。
//    m   ... F[] の配列サイズ。
//    x[] ... F[] を計算する独立変数の配列。
//    l[] ... l[i] は x[i] の下限値。指定しなかった場合は NULL がセットされます。
//    u[] ... u[i] は x[i] の上限値。指定しなかった場合は NULL がセットされます。
//    n   ... x,l,u の配列サイズ。
//
// 戻り値
//    0 ... 正常終了。何らかのエラーが発生した場合は負の（自分で判別可能な）エラーコードをリターンしてください。
//          ゼロ以外の値を返すと、.Net 側で例外が発生します。
//          正の戻り値は、NonlinearEquations クラスが独自に使用するので、できるだけ負の値を使用してください。
//
MOL_DEF_NONLINEAR_EQUATIONS
	Logistic(PTR P[],int nPtr,double F[],int m,double x[],double l[],double u[],int n)
{
    // ロジスティック曲線： yi = a/(1+b・exp(-c・xi))
	double a = x[0];
	double b = x[1];
	double c = x[2];
	DATA_POINT *pt = (DATA_POINT*)MOL_GET_COMPLEX_ARRAY_PTR(P);
	for(int i=0;i<m;++i)
	{
		double xi = pt->x;
		double yi = pt->y;
		F[i]      = yi - a/(1.0+b*exp(-c*xi));
		++pt;
	}
	return 0; // 正常終了
}

第一引数 P[] は .Net との情報交換用に用意されていて、Mol.h 内で以下のように定義されています。


//
// ユーザ定義の非線形連立方程式計算関数（MOL_NONLINEAR_EQUATIONS）の第一引数から各種情報を得るためのマクロ定義。
//
#define MOL_GET_INTEGER_ARRAY_PTR(P) ((int*)P[0])         // NonlinearEquations.TagInt プロパティの整数配列
#define MOL_GET_DOUBLE_ARRAY_PTR(P)  ((double*)P[1])      // NonlinearEquations.TagDouble プロパティの実数配列
#define MOL_GET_COMPLEX_ARRAY_PTR(P) ((MOL_COMPLEX*)P[2]) // NonlinearEquations.TagComplex プロパティの複素数配列
#define MOL_GET_EPS_ARRAY_PTR(P)     ((double*)P[3])      // NonlinearEquationsで使用される各種判定定数を格納した配列
#define MOL_GET_LOWER_BOUND_PTR(P)   ((double*)P[4])      // NonlinearEquations.MinimizeNorm() メソッドに渡された解の下限値を格納する配列
#define MOL_GET_UPPER_BOUND_PTR(P)   ((double*)P[5])      // NonlinearEquations.MinimizeNorm() メソッドに渡された解の上限値を格納する配列
#define MOL_GET_MODULE_HANDLE(P)     ((HANDLE)P[6])       // ユーザ定義DLLのモジュールハンドル

NonlinearEquations クラスのコンストラクターにネイティブDLL(NativeDllオブジェクト)と目的関数名("Logistic")を指定すれば、準備完了です。具体的には以下のようになります。


NativeDll dll = new NativeDll("UserNative.Dll");
NonlinearEquations eq = new NonlinearEquations("Logistic", dll)
eq.MinimizeNorm(x, F);

.Net とネイティブ DLL の情報交換は、.Net とネイティブな C/C++ Dll インタフェース等を参照してください。

以下の例は、ネイティブDLLとデリゲートを指定するケースを記述しています。
TestNonlinearEqs() メソッドは、境界条件あり／無しの両ケースを計算しています。


public void Test()
{
    //
    // ユーザ作成のネイティブDLL(UserNative.Dll)をロード
    NativeDll dll = new NativeDll("UserNative.Dll");

    // ロジスティック曲線の非線形連立方程式計算クラスのインスタンス作成
    NonlinearEquations eqDll  = new NonlinearEquations("Logistic", dll); // ネイティブDLLで目的関数を指定する場合
    NonlinearEquations eqDele = new NonlinearEquations(Logistic);        // デリゲートで目的関数を指定する場合

    TestNonlinearEqs("ネイティブ DLL によるパラメータ推定",eqDll);
    TestNonlinearEqs("delegate によるパラメータ推定",eqDele);
}

private void TestNonlinearEqs(string Title,NonlinearEquations eq)
{
    T.P(Title);
    //
    // ロジスティック曲線の当てはめ：  y = a/(1+b・exp(-c・x))
    //
    // 　与えられた (x,y) の点列が、上記曲線に当てはまるとして、３つのパラメータ a,b,c を計算する。
    //   以下のプログラムでは、実際に求めるのは a,b,c で、これを x[1],x[2],x[3] に割り当てています。
    //   また、予め与える点列は (x,y) のペアとして複素数のベクトルを便宜上都合が良いので用いています。
    //
    int n = 3; // 求めるパラメータ a,b,c をx[1],x[2],x[3]とする。
    int m = 15; // (x,y) の点列数を１５個とする。
     VectorDenseDouble        F = new VectorDenseDouble(m); // 関数値を格納するためのベクトル。
    //  F[i] = y - f(x)   ここで、(x,y) は以下で発生させている点列。 
    VectorDenseDouble        x = new VectorDenseDouble(n); // a,b,c が x[1],x[2],x[3] に対応
    // (x,y) 点列、便宜上複素数ベクトルを利用する。
    VectorDenseComplex       pt = new Mol.VectorDenseComplex(m);
    //
    // 先に a,b,c を固定して点列を発生させます。
    // 任意の初期値を x[1],x[2],x[3] に与えて、以下の a,b,c に収束することを確認します。
    double a = 99;
    double b = 60;
    double c = 0.6;

    for (int i = 1; i <= pt.Count; ++i)
    {
        pt[i] = new Complex(i, a / (1 + b * Math.Exp(-c * i)));
    }
    eq.TagComplex = pt; // 別途作成の Logistic 関数に渡すため。

    // 初期値
    x[1] = 90;  // a の初期値
    x[2] = 65;  // b の初期値
    x[3] = 1.0; // C の初期値

    T.P("Initial X", x);
    T.P("境界条件無しの解（関数値の二乗和はゼロ）");
    eq.CallCounter = 0;
    double r = eq.MinimizeNorm(x, F);
    T.P("Final X", x);
    T.P("Initial norm=" + eq.InitialNorm);
    T.P("Final norm=" + eq.FinalNorm);
    T.P("Iterations=" + eq.IterationCount);
    T.P("Call count=" + eq.CallCounter);
    T.P("Stop Condition=" + eq.StopCondition);

    // 最終的な残差 F[] = y-f(x)　の計算
    eq.ComputeEquations(x, F);
    T.P("F.Norm=" + F.Norm2());
    T.P("残差：", F);

    //
    T.P("境界条件付きの解（関数値の二乗和は非ゼロ）");
    x[1] = 90;  // a の初期値
    x[2] = 65;  // b の初期値
    x[3] = 1.0; // C の初期値
    //
    // x[] の上下限
    VectorDenseDouble LOW = new VectorDenseDouble(3);
    VectorDenseDouble UP = new VectorDenseDouble(3);
    LOW[1] = 89; UP[1] = 98;
    LOW[2] = 61; UP[2] = 66;
    LOW[3] = 0.5; UP[3] = 1.1;

    eq.CallCounter = 0;
    r = eq.MinimizeNorm(x, LOW, UP, F);
    T.P(" x の下限", LOW);
    T.P(" x の上限", UP);
    T.P("Final X", x);
    T.P("Initial norm=" + eq.InitialNorm);
    T.P("Final norm=" + eq.FinalNorm);
    T.P("Iterations=" + eq.IterationCount);
    T.P("Call count=" + eq.CallCounter);
    T.P("Stop Condition=" + eq.StopCondition);

    // 最終的な残差 F[] = y-f(x)　の計算
    eq.ComputeEquations(x, F);
    T.P("F.Norm=" + F.Norm2());
    T.P("残差：", F);
}

結果は以下のようになります。


ネイティブ DLL によるパラメータ推定
Initial X
   90.000   65.000    1.000

境界条件無しの解（関数値の二乗和はゼロ）

Final X
   99.000   60.000    0.600

Initial norm=75.8063687011283
Final norm=1.94516079536297E-11
Iterations=5
Call count=37
Stop Condition=MINIMUM_NORM
F.Norm=1.94516079536297E-11
残差：
    0.000    0.000    0.000    0.000    0.000    0.000    0.000    0.000    0.000
    0.000    0.000    0.000    0.000    0.000    0.000

境界条件付きの解（関数値の二乗和は非ゼロ）
 x の下限
   89.000   61.000    0.500
 x の上限
   89.000   61.000    0.500
Final X
   98.000   63.814    0.613
Initial norm=75.8063687011283
Final norm=1.71356293173386
Iterations=9
Call count=70
Stop Condition=NO_CHANGE
F.Norm=1.71356293173386
残差：
    0.161    0.219    0.263    0.255    0.145   -0.064   -0.271   -0.323   -0.176
    0.085    0.354    0.573    0.729    0.833    0.899

delegate によるパラメータ推定
Initial X
   90.000   65.000    1.000
境界条件無しの解（関数値の二乗和はゼロ）
Final X
   99.000   60.000    0.600
Initial norm=75.8063687011283
Final norm=1.94516079536297E-11
Iterations=5
Call count=37
Stop Condition=MINIMUM_NORM
F.Norm=1.94516079536297E-11
残差：
    0.000    0.000    0.000    0.000    0.000    0.000    0.000    0.000    0.000
    0.000    0.000    0.000    0.000    0.000    0.000

境界条件付きの解（関数値の二乗和は非ゼロ）
 x の下限
   89.000   61.000    0.500
 x の上限
   98.000   66.000    1.100
Final X
   98.000   63.814    0.613
Initial norm=75.8063687011283
Final norm=1.71356293173386
Iterations=9
Call count=70
Stop Condition=NO_CHANGE
F.Norm=1.71356293173386
残差：
    0.161    0.219    0.263    0.255    0.145   -0.064   -0.271   -0.323   -0.176
    0.085    0.354    0.573    0.729    0.833    0.899