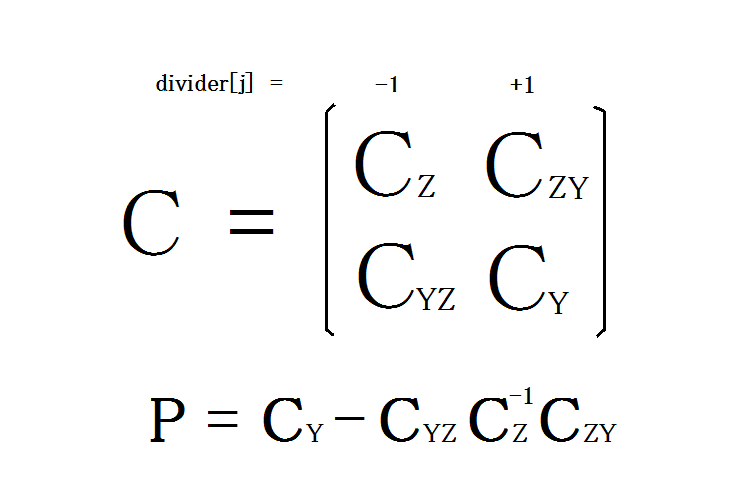フーリエ変換
フーリエ変換
多次元フーリエ変換
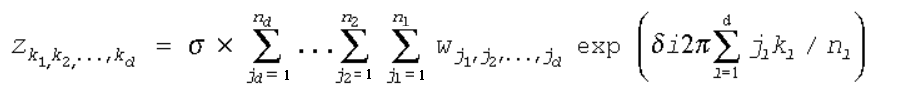
 特殊関数
特殊関数

 乱数関数
乱数関数
乱数の確率分布関数定義
確率密度関数: f(x)
離散確率関数: P(x)
累積分布関数: F(x)
 連続分布乱数発生メソッド(クラス:RandomNumber)
連続分布乱数発生メソッド(クラス:RandomNumber)
一様分布: GenerateUniform(VectorDenseDouble y, double a, double b)
a < b
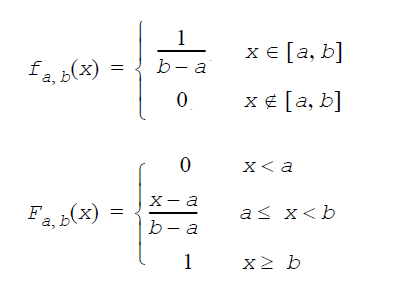
正規分布: GenerateGaussian(VectorDenseDouble y, double a, double σ, GAUSSIAN_METHOD method)
a は平均値、σ は標準偏差(σ>0)
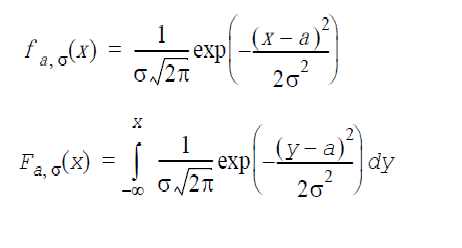
指数分布: GenerateExponential(VectorDenseDouble y, double a, double β)
a は位置因子、β は尺度因子(β>0)
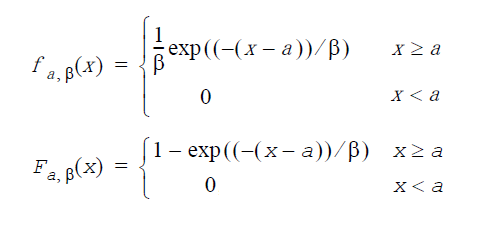
指数分布: GenerateLaplace(VectorDenseDouble y, double a, double β)
a は平均値、β は尺度因子(β>0)、標準偏差(σ)はσ = β・21/2で計算される。
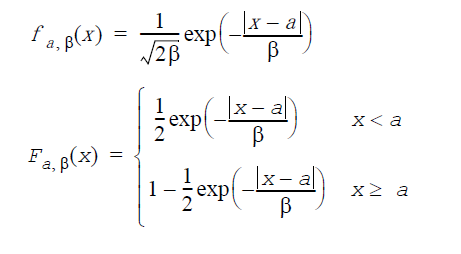
ワイブル分布: GenerateWeibull(VectorDenseDouble y, double a, double α,double β)
a は位置因子、α は形状因子、β は尺度因子(α>0、β>0)
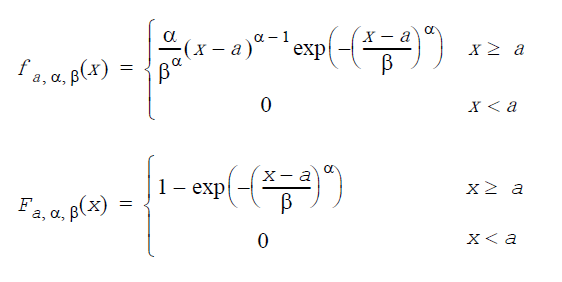
コーシー分布: GenerateCauchy(VectorDenseDouble y, double a, double β)
a は位置因子、β は尺度因子(β>0)
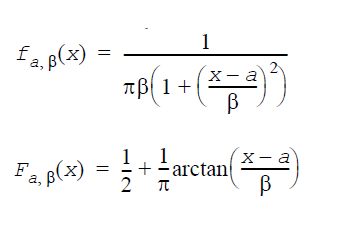
レイリー分布: GenerateRayleigh(VectorDenseDouble y, double a, double β)
a は位置因子、β は尺度因子(β>0) ※Weibull 分布で形状因子 α = 2 の分布がレイリー分布となる。
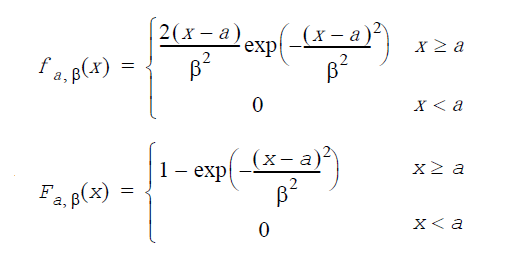
対数正規分布: GenerateLognormal(VectorDenseDouble y, double a, double σ, double b,double β,LOGNORMAL_METHOD method)
a は平均値、σ は正規分布の標準偏差(σ>0)、b は位置因子、β は尺度因子(β>0)
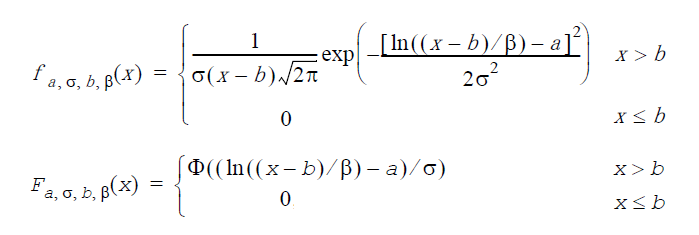
ガンベル分布:GenerateGumbel(VectorDenseDouble y, double a, double β)
a は位置因子、β は尺度因子(β>0)
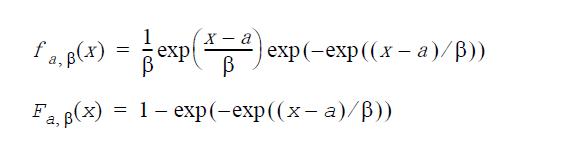
ガンマ分布:GenerateGamma(VectorDenseDouble y, double α, double a, double β)
α は形状因子、 a は位置因子、β は尺度因子(β>0)
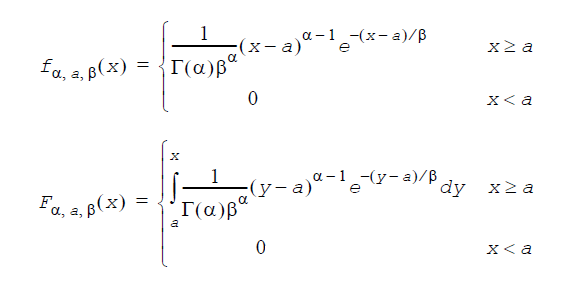
ベータ分布: GenerateBeta(VectorDenseDouble y, double p, double q, double a, double beta)
p と q は形状因子(p>0、q>0)、a は位置因子、β は尺度因子(β>0)
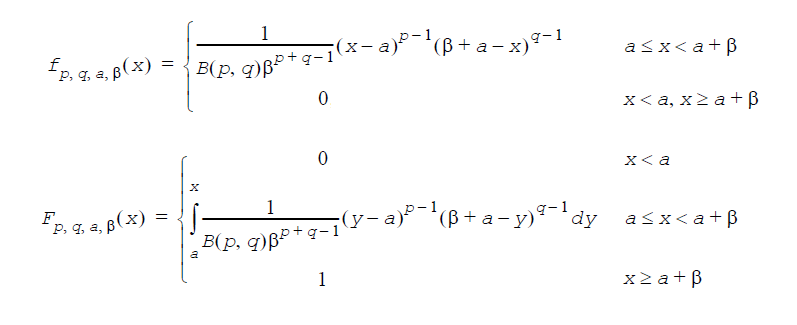
 離散分布乱数発生メソッド(クラス:RandomNumber)
離散分布乱数発生メソッド(クラス:RandomNumber)
一様分布: GenerateUniform(VectorDenseDouble y, int a, int b)
a < b
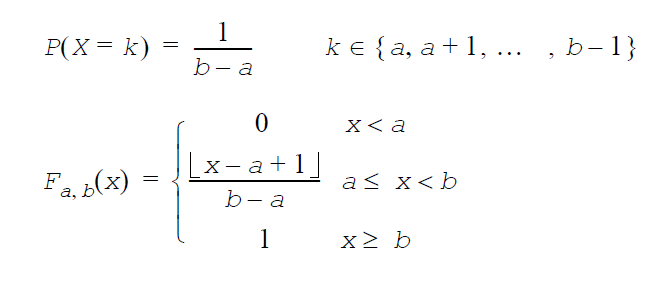
ベルヌーイ分布: GenerateBernoulli(VectorDenseDouble y,double p)
p は単一の試行成功確率(0 ≤ p ≤ 1)
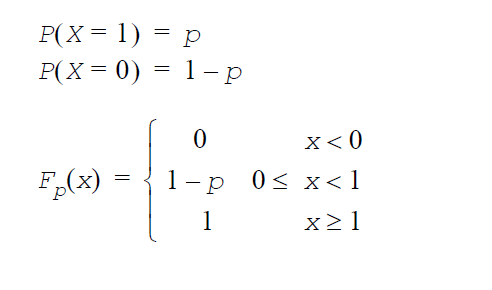
幾何分布:GenerateGeometric(VectorDenseDouble y, double p)
p は試行成功確率(0 < p < 1)
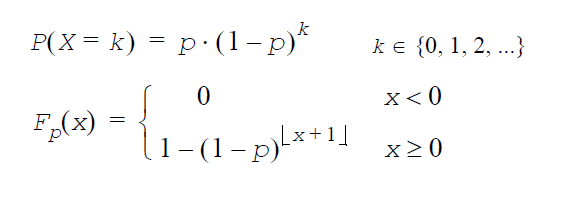
二項分布:GenerateBinomial(VectorDenseDouble y,int m, double p)
m はベルヌーイ試行回数、p は試行成功確率(0 ≤ p ≤ 1)
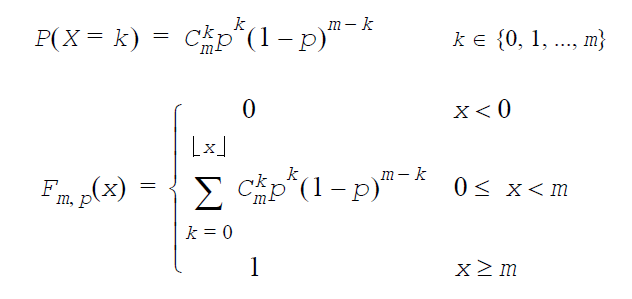
超幾何分布:GenerateHypergeometric(VectorDenseDouble y, int l, int s,int m)
l は母集団の大きさ、s は抽出の大きさ、m は母集団内の「あたり」の成分数。
※仮定:母集団(l個)は、m 個の 「あたり」l-m 個の「はずれ」で構成されている。
※k は抽出した s 個の中の「あたり」数。
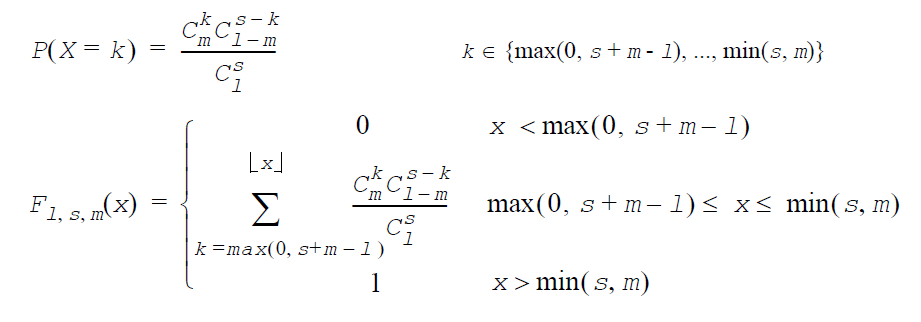
ポアソン分布:GeneratePoisson(VectorDenseDouble y, double λ,POISSON_METHOD method)
λ は分布パラメーター(λ>0)。
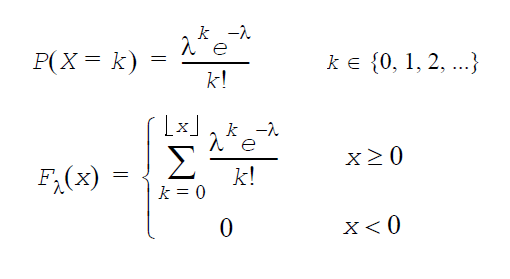
ポアソン分布(複数パラメーター): GeneratePoissonV(VectorDenseDouble y,VectorDenseDouble λ)
λi は分布パラメーター(λi>0)。
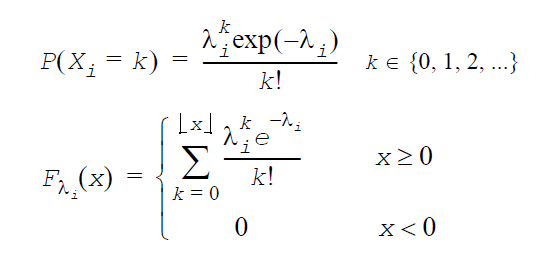
負の二項分布: GenerateNegbinomial(VectorDenseDouble y, double a, double p)
a と p は分布パラメーター(0<p<1、a>0)
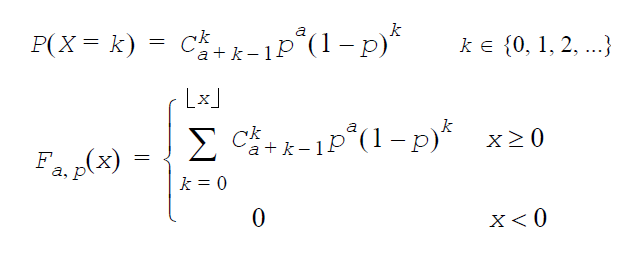
 基本統計
基本統計
重み
各重みはゼロ(を含む)以上でなければなりません。ゼロなら対象のレコードは計算から除外されます。 全ての重みがゼロは許されません。
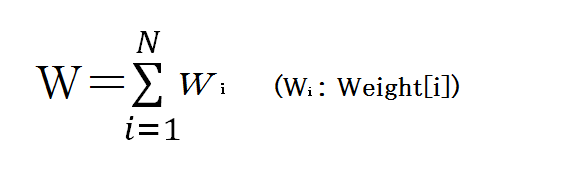
平均値
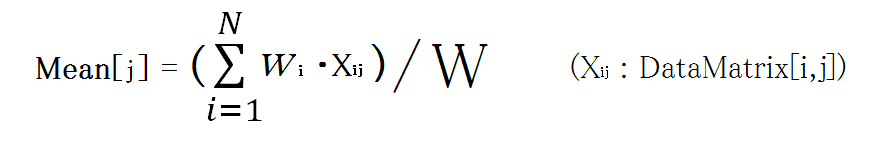
分散
分散は「不偏分散」(全ての重みが 1 の時は自由度 N-1)で2次の中心積率とは一致しません。
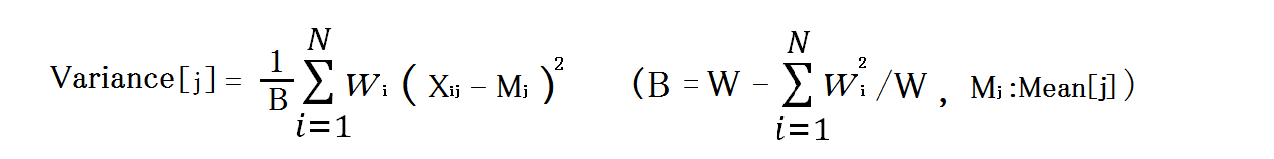
積率
積率は「代数積率」とも言います。
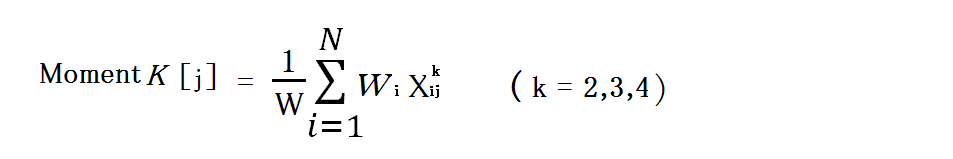
中心積率
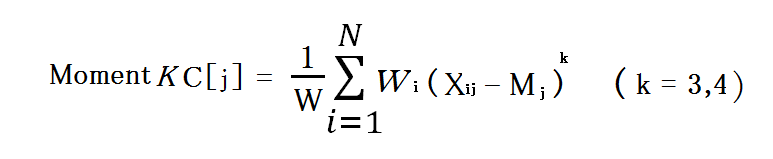
歪度

尖度

変動係数
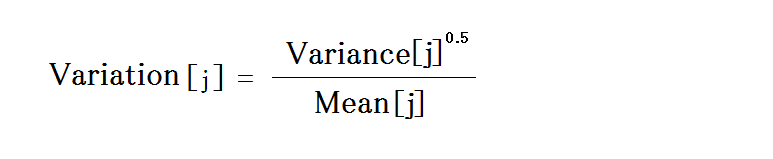
分散共分散行列
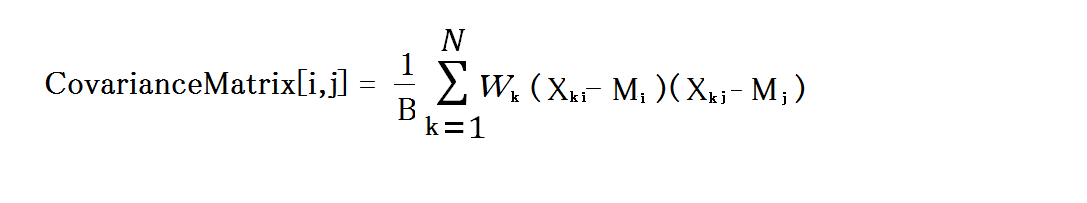
相関行列
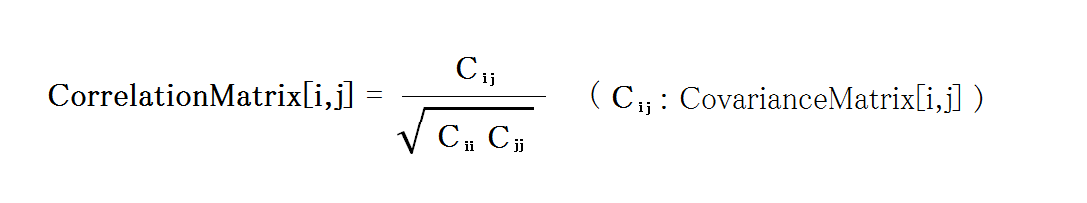
部分分散行列(P)
部分分散行列と部分相関行列は ComputePartialCovarianceCorrelationMatrix(......, divider) の引数 divider(要素の値は -1 か +1) に応じて元の分散行列の各列を -1 なら左に、+1 なら右に並べ替えます(対称性を保つために行も同時に入れ替えます)。 その後、以下のように行列を分割します。 C が元の分散(共分散)行列、 P が部分分散行列です。部分相関行列は各部分分散行列の要素から相関行列の定義通りに計算されます。