エクセル連携例（主成分分析）

Mol はエクセル等では扱うことが困難な程の大規模計算を C# 等から簡単に扱えるようにしたものです。とはいえ、計算結果の整理や結果の表示・印刷にエクセルは 非常に便利です。例題では、既存のエクセルファイルを指定して（必要なら新規にエクセルを起動します）、そのセル領域と Mol のベクトルや行列データを やり取りします。

※VBAやマクロでエクセルは大幅な機能追加、処理の自動化を実現できます。しかし、VBAやマクロを含むエクセルファイルは ウィルスに感染しているとみなされる場合があります。また、VBAやマクロはファイル単位で保存されるため、同じVBAやマクロを含むファイルが複数ある場合は修正が面倒になります。 従って、本例のようにVBAやマクロと同等（以上）の機能をエクセルファイルの外側で用意（操作）することは意味のあることです。

エクセルの準備

次に、Visual Studio を起動して、［参照の追加］ウィンドウを表示、［COM］タブを選択し、「Microsoft Excel xx Object Library」を選択します。 ここで、xx はインストールされているエクセル（オブジェクト）のバージョン番号になります。 最終的に、ソリューション・エクスプローラの「参照設定」のツリーに「Microsoft.Office.Core」と「Microsoft.Office.Interop.Excel」が表示されればプログラミング準備完了です。

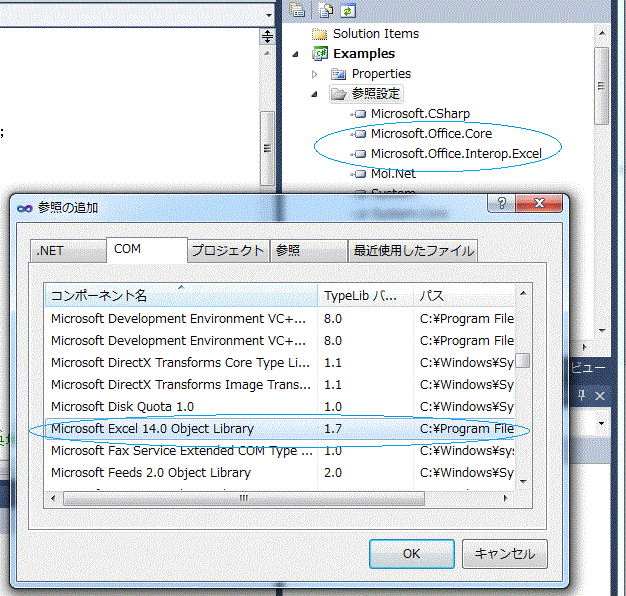例題では既に Microsoft Excel 2010 への参照（Microsoft Excel 14.0 Object Library）が追加されています。 もし、インストールされているエクセルのバージョンが異なるとき（でコンパイルや実行時に問題が発生する場合）には一旦参照を削除してから再度追加してください。エクセルのバージョンが少々異なってもプログラムコードは共通に使用可能のはずです。

ExcelTool クラス

最初に ExcelTool クラスのインスタンスを作成します（引数に既存のエクセルファイルのパスを指定します）。

   ExcelTool excel_tool = new ExcelTool("c:\\test\\sample.xlsx");

   Workbook wb = excel_tool.Book;

   Worksheet ws = (Worksheet)wb.Sheets["Sheet1"];

   // エクセルのセル "L4" からベクトル V1 を右横、"L8" から行列 M1 を右下、に向けて書き込みます。
   excel_tool.SaveVector(V1, ws.Range["L4"], true);
   excel_tool.SaveMatrix(M1, ws.Range["L8"]);

例題（主成分分析）解説

• MolExample32.exe か MolExample64.exe を実行すると、以下の図のように、各種テスト機能のボタンダイアログが表示されます。
• 「EXCEL」ボタンをクリックすると「データ読込み」と「計算」ボタンのみの小さなダイアログが表示されます。
• 「データ読込み」ボタンをクリックするとエクセルシート上の「分析対象成績データ」領域のデータを行列に読み込みます。
• 「計算」ボタンをクリックすると各種基本統計量と主成分（第１、第２）がエクセルシートに書き込まれます。

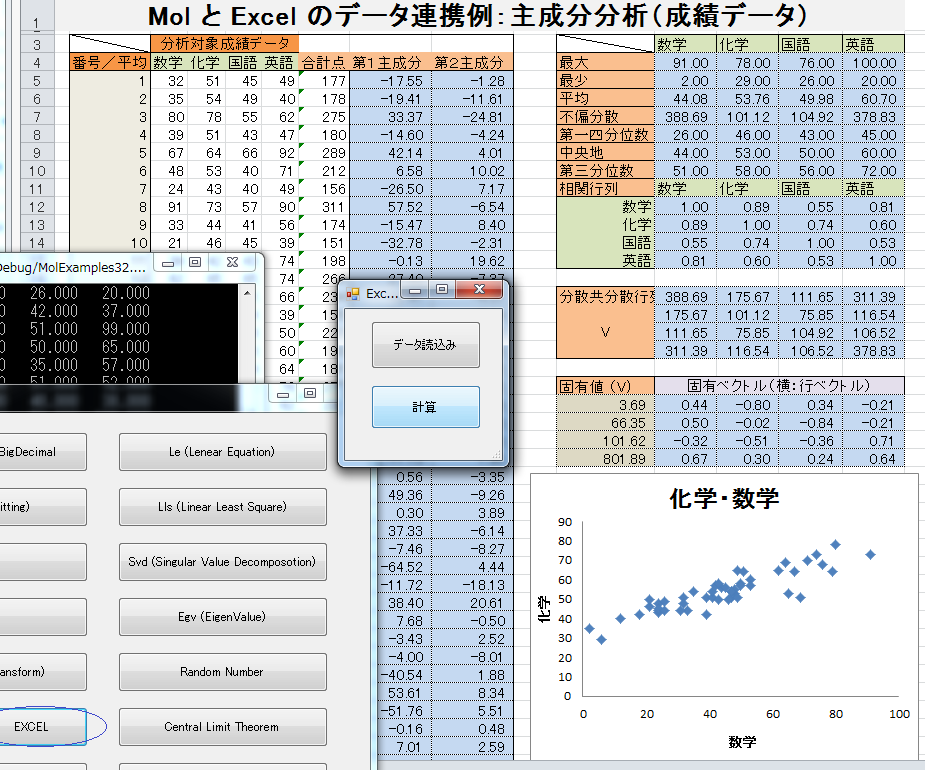
Molの基本統計（Stat）と固有値分解（EgvSolver）クラスによる主成分分析解説

主成分分析の詳細は参考書等に譲るとして、ここでは簡単に説明します。 たとえば、数学と化学の散布図をみると両科目には明らかに正の相関があります。 そこで、まず、 座標原点を各科目の重心（平均）に移動し、変位　x_i（＝データ値 － データの平均値、i=1,…,4）を処理の対象に考えます。 そして、４種の重み付き指標を新たに導入します（同じ x を用いますが、以下の x は平均からの変位を意味します）。

y1 = x1e11 + x2e12 + x3e13 + x4e14
y2 = x1e21 + x2e22 + x3e23 + x4e24
y3 = x1e31 + x2e32 + x3e33 + x4e34
y4 = x1e41 + x2e42 + x3e43 + x4e44

この e_ij をうまく設定することでデータ全体の見通しをよくする（y_i同士の関連性・相関を無くす）というのが主成分分析の第一ステップです。

まず、添え字を簡単にするために列ベクトル ei = [e1i,e2i,e3i,e4i]T を導入して
y = x1e1 + x2e2 + x3e3 + x4e4
e_i は列ベクトルなので、行列 E = (e1,e2,e3,e4) として、データ行列 X は変換により、新しい データ行列 Y に Y = XE と変換されます。

e_i に正規直交単位ベクトル（e_i・e_i=1、e_i・e_j=0 i≠j、よって E は直交行列）を選択して（各変数の平均値を原点とした）重心を中心に回転することを考えます。 では、どのように回転するのかが問題になりますが、得点データの分散・共分散行列(V)の固有値分解と結びつけることができます（相関行列を使用することも考えられます）。 すなわち

Vei = λiei (i=1,…,4)

とする固有ベクトル ei を新たな座標軸（の基底単位）とします。

行列 V に E を掛けることで V が対角化（直交ベクトル e は固有ベクトルなので E-1VE = λ、λ は対角行列でλ_iが対角成分）されることに注意してください。対角要素以外がゼロなので、新たな y 同士は無相関になります。 また固有値の性質から x の分散の和（Vの対角要素の和）と y の分散の和（固有値の和）は同じ値になります（回転だけなので原点からのばらつき全体は変化しません）。 この固有値（４つ）の最大値（yの分散の最大値）に対応する固有ベクトルに対応する y の値を第一主成分、次の値に対応する値を第二主成分…と言います。 V は対称行列で対角成分（分散）は必ず正の値ですので、固有値の性質から、V は正定値行列です。

データ行列（各要素は平均からの変位に変換したもの）を X とすれば、X の分散共分散行列 V は V = XTX と表現（自由度で除する部分などは無視）されます。
Y = XE の分散共分散行列 V_y は Vy=YTY = ETXTXE = E-1VE =>λ、 V_y を対角行列 λ に変換することは V の固有値問題（VE=Eλ）に帰着されます。

固有値（λ の対角要素）の値が極端に異なる場合、固有値の大きい主成分だけである種の判断情報を得るのが主成分分析の目的になります。

例題では基本統計量の計算は　Mol の Statクラス、固有値分解には EgvSolver クラスを使用しています（もちろん、エクセルにも同様な機能は備わっています）。

以下、例題より抜粋

　   // データ行列
     MatrixDenseGeneralDouble Mat = new MatrixDenseGeneralDouble(50, 4);

     // m_bookTool は ExcelTool オブジェクト、m_stat は Stat オブジェクト
     m_bookTool = new ExcelTool(m_xlsFile);
     m_stat     = new Stat(Mat);

     VectorDenseDouble QuantileOrder = new VectorDenseDouble(3); // 分位率
     // j 番目の（列）データ平均値は m_stat.Mean[j] という形で得られますが中央地は、以下のように m_stat.QuantileOrder に
     // 0.5 を指定した部分(i=2) に格納されます。従って、 j 番目の（列）データの中央地は m_stat.QuantileMatrix[2,j] になります。
     QuantileOrder[1] = 0.25;
     QuantileOrder[2] = 0.5;  // 中央地
     QuantileOrder[3] = 0.75;
     m_stat.QuantileOrder = QuantileOrder;

     m_stat.Computed = Stat.PROPERTIES.ALL;

     // m_xlsFile をオープンしているエクセルに連結します（存在しなければエクセルを起動）
     Workbook wb = m_bookTool.Book;
     Worksheet ws = (Excel.Worksheet)wb.Sheets[m_sheetName];

     // シートからデータ行列を Mat に読み込む
     m_bookTool.LoadMatrix(Mat, ws.Range["C5"]);

     // シートから読み込んだデータから基本統計量を計算
     m_stat.ComputeProperties();


     // 基本統計量をエクセルシートに書き込む
     m_bookTool.SaveVector(m_stat.Max, ws.Range["L4"], true);
     m_bookTool.SaveVector(m_stat.Min, ws.Range["L5"], true);
     m_bookTool.SaveVector(m_stat.Mean, ws.Range["L6"], true);
     m_bookTool.SaveVector(m_stat.Variance, ws.Range["L7"], true);

     m_bookTool.SaveMatrix(m_stat.QuantileMatrix, ws.Range["L8"]);
     m_bookTool.SaveMatrix(m_stat.CorrelationMatrix, ws.Range["L12"]);
     m_bookTool.SaveMatrix(m_stat.CovarianceMatrix, ws.Range["L17"]);

     // 固有値分解
     MatrixDenseSymmetricDouble A = (MatrixDenseSymmetricDouble)m_stat.CovarianceMatrix.Clone();
     EgvSolver es = EgvSolver.Solve(null,null,A);
     m_bookTool.SaveVector((VectorDenseDouble)es.EigenValues, ws.Range["K23"], false);
     m_bookTool.SaveMatrix((_MatrixDouble)_Matrix.Transpose(null, (_MatrixDouble)es.EigenVectors), ws.Range["L23"]);

     // 第一主成分
     MatrixDenseGeneralDouble vecs = (MatrixDenseGeneralDouble)es.EigenVectors;
     VectorDenseDouble mean = m_stat.Mean;
     // 主成分ベクトル 
     VectorDenseDouble C = new VectorDenseDouble(Mat.RowCount);

     // 第一主成分をエクセルシートに書き込む（Matはデータ行列）。
     for (int i = 1; i <= Mat.RowCount; ++i)
     {
         double s = 0;
         for(int j=1;j<=Mat.ColumnCount;++j)
         {
            s += vecs[j,4] * (Mat[i, j] - mean[j]);
         }
         C[i] = s;
     }
     m_bookTool.SaveVector(C, ws.Range["H5"], false);

     // 第二主成分をエクセルシートに書き込む。
     for (int i = 1; i <= Mat.RowCount; ++i)
     {
         double s = 0;
         for (int j = 1; j <= Mat.ColumnCount; ++j)
         {
             s += vecs[j, 3] * (Mat[i, j] - mean[j]);
         }
         C[i] = s;
     }
     m_bookTool.SaveVector(C, ws.Range["I5"], false);