Mol は以下の２つの DLL から構成されています。

1. Mol.Net.Dll ... .Net のクラスライブラリーです。

2. Mol.C++.Dll ... ベクトルや行列相互の演算等を実行します。また、連立方程式解法時などには MKLと情報をやり取りします。

Mol.C++.Dll は C++ で記述された通常の DLL です（.Net専用のマネージドコードではありません）。

ベクトルや行列等のメモリー領域は Mol.C++.Dll で管理されます。

Mol.Net.Dll で提供される全てのクラス（Mol オブジェクトと呼びます）は_Molクラスを基底に持ちます。

Mol オブジェクトで（'_Mol'のように）アンダースコアーで開始するクラス名を持つものは全て抽象クラスです。各種のスタティックなメソッドを提供していますが、独自に継承してインスタンス化しても意味がありません（クラッシュする可能性もあります）。

_Mol クラスは全ての Mol オブジェクトに Dispose() メソッドを提供しています。 Dispose() メソッドは Mol.C++.Dll で確保されたメモリー領域を解放します。 当然ながら全ての Mol オブジェクトは .Net のガベージコレクションによって、使用されなくなれば自動的にメモリーから解放されます（この時、Mol.C++.Dll で確保されたメモリー領域も解放されます）。 しかしながらガベージコレクションによって解放される時期は予め予測できません。 特に大きなメモリー領域を消費する行列等は使用しなくなったら積極的に Dispose() メソッドを呼び出すことをお勧めします。 自分で Dispose() メソッドを呼び出すか、以下の例のように using ステートメントを使用します。

コードをコピー

// 自分でメモリーを解放する例。 MatrixDenseGeneralComplex A = new MatrixDenseGeneralComplex(100,100); try { // 計算処理 ....................................... } finally { // A を使用しなくなったら、積極的にメモリーを解放する。 A.Dispose(); } // コンパイラーに Dispose() を呼び出すように指示する例。 using (MatrixSparseGeneralComplex B = new MatrixSparseGeneralComplex(100,100)) { // 計算処理 ....................................... // この using ブロックを抜けるときに自動的に B.Dispose() が呼ばれます。 }

Mol は巨大な行列や大量データを高速に処理（計算）する様々な手法を提供しています。 LightDB（LightDB<(Of <(<'K, D>)>)>）は Mol が 扱うデータを素早く格納・検索して計算処理を側面から支援するために時別に設計された軽量データベースクラスです。 既に多くのデータベースシステム（Oracle,SQL Server,PostgreSQL 等の 'DBMS'）が存在し、データの安全な保全と SQL を使用した柔軟な データ格納・検索機能が提供されています。多くの場合、データの管理は、これら DBMS を前提に管理されるべきです。 しかし、多くの DBMS はその大型、かつ、頑健さと柔軟性故に逆に「簡便性」に欠けることも事実です。 LightDB は SQL による柔軟な検索などには対応していませんが、要求メモリーも少なく（それでも数十Ｇバイト以上のデータでも高速処理可能です）、 別途 DBMS を稼働させる必要がありません。 全データ自体は DBMS で管理し、必要な部分を LightDB に移して計算処理するような形態がベストな選択になると思います。

LightDB は多くの DBMS が高速検索を実現するために作成する、 B-Tree 構造（平衡多分木）を持った、インデックスの機能を Mol に 組み込んだものです。LightDB のレコードは先頭に（レコードの順番を決める）キーフィールド、次にデータフィールドが続く単純な 構造です。キーフィールドとデータフィールドは、それぞれ sbyte、byte、short、ushort、int、uint、long、ulong、float、double、Complex、string のどれか一つの配列となります。ただし、 string は一個で ushort の配列として扱われます。また、 complex は実数部と虚数部が繰り返す double の配列と扱われます。 一つの LightDB ファイルのレコードは２つの（キーとデータ）タイプの配列から構成されることになります。

各レコードはキーフィールドの大小関係に従って自動的に（B-Tree 構造に）並べ替えられます。（ソートされると考えても可です。 　大小関係の決定はキーフィールド配列の先頭から単純に比較します。） 任意のキーを指定した検索は高速に実行されます。 また、処理したレコードの位置はレコードポインターに格納され、そのレコードからの（大小関係に応じた）順次処理も簡単にできます。

LightDB の概要や使用例等は Let's 'C#で数値計算' with Mol ＆ Dsl を参照してください。

.Net では既に Decimal が用意されていて、double では有効桁数が足りない場合に使用することができます。 Decimal で扱える有効桁数 28 ～ 29 位です。 一方、BigDecimalはメモリー容量と計算時間の許す限り任意の桁数まで計算することができます(計算速度はより遅くなります)。

定義

BigDecimal を作成するには BigDecimal a = new BigDecimal("1.23456"); や BigDecimal a = BigDecimal.Parse("1.23456E-10"); というふうに記述します。指定する数値表現文字列は、通常の double 値を表現する文字列と同じです。もちろん、任意の長さを記述可能です。

有効桁数

BigDecimal の標準的な数値表現（出力）形式は 0.zxxxxxxxxzE±eeee となります。 ここで z はゼロ以外 1～9 の数字、x は 0～9 の数字になります。zxxxxxxxxz は任意の長さ（有効桁数）を指定できます。 BigDecimalで定義している有効桁数（zxxxxxxxxzの文字数）は一般的に使用される「有効数字」や「有効桁数」と若干が異なります。 eeee は指数部（基数は10）で、整数(int)で表現可能な範囲となります。

四則演算（+ - * /）

割り算（/）を除く演算(+ - *）は必ず正確な計算が最後まで実行され、途中で計算が打ち切られることはありません（デフォルトの動作）。 一方、 1/3 の例を出すまでもなく、多くの割り算は途中で計算を打ち切る必要があります。 c = a / b; の計算では c の有効桁数 = a の有効桁数 + b の有効桁数 + double の有効桁数 程度になります。いずれにしても四則演算（+ - * /）を繰り返すと結果の有効桁数が大幅に増えて計算時間が長くなると同時に多くのメモリーを消費する可能性があります。

丸め操作

有効桁数が不必要に長くなる場合、途中で計算を打ち切り、丸める操作が必要です。MaxDigitsプロパティに値をセットすることで、 全ての四則演算の最大有効桁数を指定することができます。BigDecimal.MaxDigitCount プロパティのデフォルト値は 0 で、最大有効桁数は無制限を意味します。 個々の演算の指定した桁位置で計算を打ち切り、丸めるにはスタティックなメソッド Add(BigDecimal, BigDecimal, BigDecimal, Int32)Sub(BigDecimal, BigDecimal, BigDecimal, Int32)Mul(BigDecimal, BigDecimal, BigDecimal, Int32)Div(BigDecimal, BigDecimal%, BigDecimal, BigDecimal, Int32) 等を利用します。 また、任意の BigDecimal 値を任意の桁位置で丸める（スタティック・インスタンス）メソッドとして PointRound() と LengthRound() の２つが用意されています。 PointRound(BigDecimal, Int32, BigDecimal..::..ROUND_MODE) は小数点の位置から右または左の（相対的な）指定位置を丸めます。 LengthRound(BigDecimal, Int32, BigDecimal..::..ROUND_MODE) は有効桁の左端からの桁位置を指定して丸めます。 丸め方法も、四捨五入・切り捨て・切り上げを含め各種用意されています。

値型と参照型

double や構造体の Complex は値型ですが、BigDecimalクラスは参照型です。 同じ数値を扱うのに double は値型で BigDecimal は参照型という些細な違いがありますが、違いが些細である故に、ミスがあると逆に発見しづらいので注意してください。

コードをコピー

// 値型の例 double a,b; a = 1.0; b = a; // 代入は '1.0' の新しいインスタンスが作成されて b に代入される（と考えて差し支えない）。 // この時点で '1.0' のインスタンスは２個ある（と考えて差し支えない）。 a = 2.0; // a の値が変化しても b の値は 1.0 のまま（別な '1.0' のインスタンスだから）。 // 参照型の例 BigDecimal x = new BigDecimal("1.0"); BigDecimal y = x; // double の例と異なり、y と x は同じ 1.0 のアドレスを保持する(b=a の動作と異なる)。 BigDecimal z = x.Clone(); // 1.0 の新しいインスタンスが作成されて z に代入される(b=a の動作と同じ)。 BigDecimal.Negate(x); // x と y は　-1.0 になるが、z は 1.0 のまま

例の Clone() （+ - * / や BigDecimal.Zero、BigDecimal.One...等も同様）のように新しいインスタンスを作成するメソッドを使用する場合は問題ありませんが、 BigDecimalでは Negate のようにインスタンスそのものを変更するメソッドもいくつか用意されていて、それらを使用する場合は注意してください （Div や Mul 等のメソッドの第一引数を指定した場合も同様）。 一般に、メソッドで（戻り値として） BigDecimal を返すもの（Div や Mul 等では第一引数に null を指定した場合）は新しいインスタンスを作成します。 一方、例の Negate はインスタンスは作成しないので注意が必要です。

数学関数

BigDecimal で（標準的に）用意されている数学関数は平方根を計算する Sqrt() のみです。 三角関数（Sin,Cos等）や Log、線形連立方程式の解法等の数学関数は可変精度という困難さにより、標準ではなくサンプルプログラムとして、 ソースコードで提供しています（BigMath.cs参照）。ソースコードは自由に編集してかまいません。 特に例題という位置付けですので、簡潔にするためエラーチェックなど全くしていない部分もあります。

与えられた N 個の（実験値や測定値の）データ列 W_j (j=0,1,2,...,N-1) について

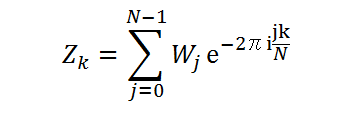
という変換を離散フーリェ変換(Forward:前進変換)といいます。 また、逆に

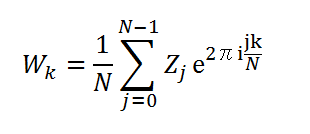
と Z から W を計算する場合をフーリェ逆変換(Backward:後退変換)といいます。

チップ：
文献などの表記に合わせて各式の添え字は 0 から開始（C形式）していますが、プログラミング時のデフォルトは 1 から開始する FORTRAN 形式です。 IndexBase をセットしてC形式に変更することも可能です。

ここで、W は実数か複素数です。一方 Z は全て複素数になります。 W が実数の場合は DftDouble クラス、複素数の場合は DftComplex クラスを使用します。

前記２式はデータが一次元のデータ列ですが、Mol（MKL）では多次元に拡張した以下の一般式を用います。

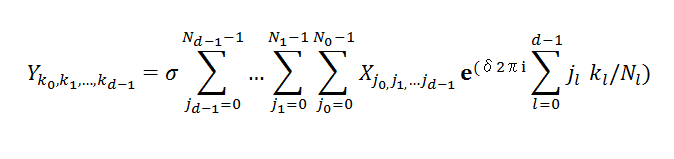
ここで i は虚数単位、d（≧1）は次元数（インデックスの数）、N_i（0≦i≦d-1）は各次元サイズ（各インデックスの最大値。 δは変換の方向を決定する因子で前進（Foward）変換の時は -1、 後退（Backward）変換の時は +1 が設定されます。Y と X には、上記 W と Z に当たる多次元の配列データを変換方向に応じて設定します。

σはスケール因子でデフォルトで前進変換のときは 1.0、後退（逆）変換の時は 1.0/(N₀・N₁・...N_d-1) が設定（変更可）されます。

重要な注意事項：
データ値の数が 2、3、5、7、11、または 13 の累乗に因数分解できる場合は高速フーリエ変換（FFT）が適用され、最大のパフォーマンスを得ることができます。

[計算手順]

１．元データが実数なら DftDouble、複素数なら DftComplex オブジェクトを作成する

DftDouble や DftComplex オブジェクトの作成時点で全てのデータのサイズを（コンストラクターへの引数で）指定します。 つまり、オブジェクトの作成時に元データと変換データの領域が全て確保されます。 以下 DftDouble と DftComplex のベースクラス _DFT オブジェクトで説明します。

２．変換元のデータを設定

元データ領域と変換データ領域は _DFT オブジェクトに確保されていますので、そこに 変換元のデータを全てセットします。前進変換なら元データ領域に SetDataValue(Double, array<Int32>[]()[][]) メソッドで値を設定します。 後退変換なら変換データ領域に SetDftValue(Complex, array<Int32>[]()[][]) メソッドで値を設定します。

３．変換計算の実行

元データ領域にデータを設定したのなら ComputeForward()()()() メソッドでフーリェ変換を実行します。計算結果は変換データ領域に書き込まれますので GetDftValue(array<Int32>[]()[][]) メソッドで取り出します。

元データ領域（X）が実数の場合、変換データ領域（Y）には以下のような性質があります（インデックスはFORTRAN形式）。

• Y_j1,j2,j3... = Complex.Conjugate(Y_{(N1-j1)%N1+1,(N2-j2)%N2+1,(N3-j3)%N3+1,....}

• 先頭要素 Y_1,1,1,... の虚数部分はゼロ（先頭要素は実数）。

• 次元サイズが偶数の場合、先頭要素から半分の位置にある要素も虚数部分はゼロ（実数）となります。

従って、元データが実数の場合の変換データ領域は複素共役部分を省略した特殊な構造を採用してメモリー領域を節約しています。

逆に変換データ領域にデータを設定した場合は ComputeBackward()()()() メソッドでフーリェ逆変換を実行します。 計算結果は元データ領域に書き込まれますので GetDataValue(array<Int32>[]()[][]) メソッドで取り出します。

チップ：
元データ領域・変換データ領域は複数設定することができます。つまり、同じサイズのデータ列を複数指定して一気に複数回の変換を計算できます。 GetDataValue() 等のメソッドでアクセスできる領域は、Page （1≦Page≦PageCount）プロパティで指定された１領域に限られます。

以下は実数２次元データの前進変換プログラム（イメージ）です。 データ領域は NxM 個の要素を持つ２次元データの組が P 個あります。それぞれの２次元データに対して P回の変換が（一度に）実行されます。 どの２次元データにアクセスするのかは Page プロパティで指定します。各２次元データにアクセスするインデックスはデフォルトで １ から開始します。

※Pageは常に 1≦Page≦PageCount の範囲でアクセスしますが、データのインデックスはFORTRAN（デフォルト）形式か C 形式を選択できます。

コードをコピー

const int P = 3; // ページ数 const int N = 4096; // 行数 const int M = 4; // 列数 DftDouble fft = new DftDouble(P,N,M); // ２次元行列イメージ NxM 個の要素を持つ P 個の領域を確保. // 元データ領域にデータをセット. for(int p=1;p<=fft.PageCount;++p) { fft.Page = p; // 処理対象のページをセット. for(int i=1;i<=N;++i) { for(int j=1;j<=M;++j) { double W = ..... ; // [i,j] データの取得. fft.SetDataValue(W,i,j); // p ページの元データ領域、データ位置（[i,j]）に v を設定. } } } fft.ComputeForward(); // 前進変換を実行する. // 変換データ領域から結果を取得する. for(int p=1;p<=fft.PageCount;++p) { fft.Page = p; // 処理対象のページをセット. for(int i=1;i<=N;++i) { for(int j=1;j<=M;++j) { Complex Z = fft.GetDftValue(i,j); // p ページの変換データ領域、データ位置（[i,j]）の値を取得. ..... ; // [i,j] データの処理. } } }

以下、_DFT オブジェクトのメソッドやプロパティの概念図です。

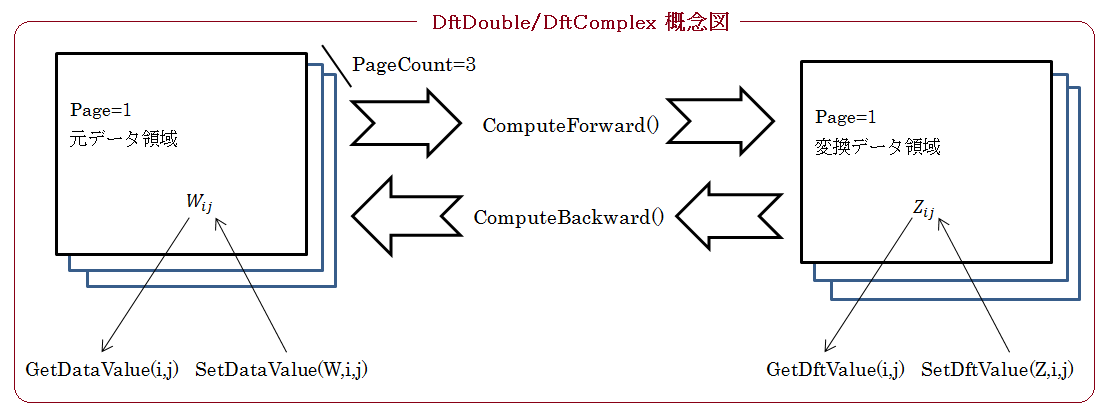
多次元のデータを変換するには上記のようにデータ領域をオブジェクト内部に確保してSetDataValue()、GetDataValue()、SetDftValue()、GetDftValue()のメソッドを 介してデータにアクセスします。変換データが一次元か２次元なら DftDouble や DftComplex オブジェクトのコンストラクターに 元データと変換データとしてベクトルか行列を指定することができます。DftDouble や DftComplex オブジェクトは指定されたベクトルや行列の参照を保存して、 元データや変換データ領域として使用します。従って、前記メソッド以外に指定したベクトルや行列のデータアクセス方法を使用できます。 この場合、元データや変換データ領域としてそれぞれ一個ずつしか指定できないので PageCount は 1 となります（ページ操作は意味がありません）。 さらに指定するベクトルや行列のサイズは一致している必要があります。

コードをコピー

int N = 1000; int M = 10; MatrixDenseGeneralDouble odata = new MatrixDenseGeneralDouble(N,M); // 元データ領域. MatrixDenseGeneralComplex tdata = new MatrixDenseGeneralComplex(N,M); // 変換データ領域. DftDouble dft = new DftDouble(odata,tdata); for(int i=1;i<=N;++i) { for(int j=1;j<=M;++j) { odata[i,j] = .... // 元データ値の設定 } } dft.ComputeForward(); // フーリェ変換（odata→tdata） for(int i=1;i<=N;++i) { for(int j=1;j<=M;++j) { tdata[i,j] .... // 変換データ（DFT）値にアクセス } }

全てのベクトルと行列は _Array クラスを継承しています。 行列はイメージ的には２次元ですが、最終的には _Array クラスが管理する一次元配列で管理されます。 例えば A を密一般行列（サイズは M x N）、Array を _Array クラスが管理する一次元配列（配列サイズは M x N になります）とすると 要素 A[i,j] は Array[M*(j-1)+i] の位置に格納されます。

注意事項：
_Array は要素を並べ替える sort() メソッドが実装されています。従って _Array を継承するベクトルなどで利用可能です。 ただし、複素数配列の sort() はサポートされません。 密なベクトル以外でも並べ替えは可能ですが、「配列」の意味を理解していないと、期待した結果は得られません。

※疎な行列では最初の代入で、代入された行列要素の領域が、_Array 上に確保されます（配列サイズは動的に増加します）。

各種の行列のメモリー管理についての詳細は Mkl のマニュアル等を参照してください。

Mkl や既存の数値計算ライブラリーは FORTRAN で記述されたものが沢山あります。 FORTRAN と C や C# との大きな違いに配列の開始インデックスがあります。 つまり、FORTRAN では配列のインデックスは 1 からですが C や C# では 0 から開始します。 また、数値解析の文献も多くの場合 1 から開始するインデックスで記述されています。 Mol ではIndexBase（スタティックなプロパティです）を適切に設定することで、この違いを吸収しています。 デフォルトでは_Array.IndexBase = INDEX_BASE.ONEとなっているので任意の行列を A とすると A[1,1] が先頭になります（FORTRANと同じです）。 _Array.IndexBase = INDEX_BASE.ZEROとすれば A[0,0] が先頭になります。 _Array.IndexBase は任意の時点で切り替えることが可能ですが、途中で切り替えるような使用方法は間違いのもとになります。

スカラー（double や Complex）、行列それにベクトル間で自由に掛け算などの四則演算が可能であることは既に記述しています。 ベクトルや行列では割り算などで制限があるのは当然ですが、基本的に演算子(+ - * /)が自由に使用できます。 これによってプログラムはすっきりと簡単になります。ただし、四則演算子を多用すると作業変数（作業用のベクトルや行列）が多く作成されるので注意が必要です。 特に行列のサイズが大きい場合はメモリー領域を圧迫することになります。

例えば C = alpha*A + beta*B (A,Bは任意の行列、alpha と beta はスカラー)では

	コードをコピー
W1 = alpha*A; // 作業行列１(W1) が新規に作成されます。 W2 = beta*B; // 作業行列２(W2) が新規に作成されます。 C = W1 + W2;

のように２つの作業行列（W1とW2）が目に見えない形で作成されます。A や B が大きなサイズの行列の場合、思わぬメモリー不足状態にならないように注意してください。

作業配列をなるべく使用しないようにするには、前記の _Blas クラスのメソッドを使用するか _Arrayクラスの四則演算メソッド(Add(),Sub(),Mul(),Div())を使用してください。 どの四則演算メソッドも第一引数に左辺変数を指定します。もし、第一引数が null なら左辺変数が作成されます。従って、第一引数に共通の作業変数を渡して同じ変数を使いまわすことができます。 （プログラム自体は若干読みづらくなります。）

	コードをコピー
MatrixDenseGeneralDouble C = (MatrixDenseGeneralDouble)_Array.Add(null,A,B); // A と B は任意の行列。第一引数が null なので C は新たに作成される。 ........................... _Array.Sub(C,X,Y) ; // X と Y は任意の行列。第一引数が C なのでX-Yの結果は C に保存される。戻り値も C になります。

注意事項：
ベクトルや行列の各四則演算メソッドや四則演算子は各要素のサイズが一致していないとエラーになります。サイズの異なる行列の掛け算も掛け算の定義通りのサイズと異なる場合はエラーになります。

Mol では様々な行列やベクトル間の掛け算などの四則演算が実装されています。 例えば、任意の行列(double)を A と B とすると

	コードをコピー
// A と B は任意の行列（例えば A が MatrixSparseSymmetric で B が MatrixDenseUpperTriangle 等‥） MatrixDenseGeneralDouble C = A * B;

のように１行で行列同士の掛け算を記述できます。もちろんベクトルと行列の掛け算も同様です。 ただし、このような全ての組み合わせに対しての演算は Mkl の専用演算ライブラリ（Blasと呼ばれます）と比べると低速になります。 そこで Mol では _Blas クラスを導入して Mkl の Blas ライブラリーを直接呼び出せるようになっています（スタティックメソッドです）。 特に計算時間が問題になるような環境で、所望な演算が _Blas 内のメソッドに存在する場合は、そちらを使う手もあります。 特にC = alpha*A + beta*Bというような形の計算は _Blas 内のメソッドで多くサポートされています。

_Blass クラスで提供されているメソッド群（行列には演算時に転置や複素共役の指定をすることができます）

• LeMv() ... y = alpha*A*x + beta*y という形の演算を実行します。ここで y はベクトル、A は行列、alpha と beta はスカラーです。

• Mv() ... y = A*y または y = A*x という形の演算を実行します。ここで x と y はベクトル、A は行列です。

一般行列・帯行列・対称行列・三角行列（上と下）、さらに密・疎な配列の内部データ構造は MKL と完全に一致しています。それぞれが組み合わさって非常に複雑な構造ですが、Mol が違いを吸収しているのでプログラミング上では特に意識する必要はありません。 ただ、計算時間には大きな違いが出てきます。密な行列（宣言時に全要素の領域が確保されます）の要素 A[I,J] は I と J の簡単な計算から直接値を出し入れできます。 従って、全ての要素に対するアクセスはほぼ同じ時間です。 これに対して、疎な行列（要素領域は代入時動的に確保されます） B[I,J] では I と J で場所を計算することはできません。 I と J は B[I,J] の名前のような扱いになります。 B[I,J] を参照する場合は「名前」をキーに要素を検索することになります。従って、要素によってアクセス時間に差が出てきます。 特に値の代入 B[I,J] = v では、見つからなかった場合に新たな場所が確保されるという動作時間が追加されます。 参照の場合で見つからなかった場合、値ゼロが返りますが場所は確保されません。検索時間を短くするために要素は I と J の値に応じて並べられます。 並べる順序は、まず J の順に、次に I の順で動的（最初の代入時）に決定されます。当然、並べられた要素列の最後尾に追加する場合は良いとして、 列に要素を挿入するような場合は挿入位置より後ろの配列要素の移動が生じます。 疎な行列要素に値を代入する方法は、以下のようなコードが効率的となります。

	コードをコピー
int N = 10; int M = 20; MatrixSparseGeneralDouble A = new MatrixSparseGeneralDouble(N,M); for(int I=1;I<=A.RowCount;++I) { for(int J=1;J<=A.ColumnCount;++J) { ......................... if(Math.Abs(v)>_Mol.EPS) A[I,J] = v; // この時点で A[I,J] の(非ゼロ)領域が確保され、IとJの順序に従って並べられる。 } }

疎な行列はランダムな要素アクセスには非効率ですが、順序に従って並んでいるので連立方程式の解法等、順序に従って要素を参照する操作では逆に効率的になります。 要素の値を参照する場合、検索して見つからない場合にゼロが返りますが、以下のように登録されている要素のみアクセスする方法もあります。 以下のコードは密な行列でも同じように動作しますが、冗長的になります。詳細はレファレンスを参照してください。

コードをコピー

MatrixSparseGeneralDouble A = new MatrixSparseGeneralDouble(n,m); ............................ for(int I=1;I<=A.RowCount;++I) { int m = A.GetRegisteredElementCount(I); // I 行に登録されている要素数. for(int j=1;j<=m;++j) { ............................ INDEX_PAIR ix = A.GetArrayIndex(I,j); // I 行の j 番目に登録されている要素の情報を取得. J = ix.Index; // J が実際の列番号 ( j は登録位置で疎な行列では列番号と一致しない。). ............................ Complex cv = A.GetElement(ix.ArrayIndex); // A[I,J] == cv.Re （Aは実数行列だから）. ............................ double v = cv.Re; // cv.Im は常にゼロ（Aは実数行列）. ............................ } }

もちろん、以下のコードでも同じ結果が得られます。

	コードをコピー
MatrixSparseGeneralDouble A = new MatrixSparseGeneralDouble(n,m); ............................ for(int I=1;I<=A.RowCount;++I) { for(int J=1;J<=A.ColumnCount;++J) { ............................ double v = A[I,J]; ............................ } }

GetRegisteredElementCount() や GetElement() メソッドはメモリー上に実際格納されている要素の個数や値を返します。 密な行列でも上三角行列・対称行列・エルミート行列では上半分、下三角行列は下半分、帯行列は帯の幅となります。 さらに、疎な行列では密な行列と同じ領域の要素に実際に代入して領域が確保された個数になります。 例えば T が密な下三角行列ならば I == T.GetRegisteredElementCount(I) が成立します。 T が疎な下三角行列ならば I >= T.GetRegisteredElementCount(I) が成立します。

チップ：
対称行列やエルミート行列では注意が必要です。対称行列やエルミート行列も上半分部分しか格納されないので動作は上三角行列と同様になります。 しかし、実際には下半分の要素が存在するので、それなりの工夫が必要です。例えば E をエルミート行列とすれば E.GetElement() で得られるのは E[I,J] で I <= J の値だけです。E[J,I] の（複素共役も含めた）操作は自分で実行する必要があります。もちろん E.GetElement() ではなく、 E[I,J] または E[J,J] という形式を用いれば気にする必要はありません。

_VML クラスには「密」なベクトルの各要素に対し同時並行的に演算を実行する各種 static なメソッドが実装されています。

例えば x,y,z を密なベクトルとして z[i] = x[i] + y[i] という演算はベクトル要素間に依存性が無いので（極端な話ですが）全ての足し算を 同時に実行可能です（もちろん利用可能スレッド数の制限があります）。ベクトル要素数が多いときはマルチスレッド機能の恩恵を十分に受けることができます。

_VML には以下のような様々な演算が用意されています：

　　・四則演算（1次分数変換や逆数、共役複素数計算等を含む）

　　・各種の丸め（切り捨て、切り上げ等）計算

　　・三角関数・双曲線関数（逆関数等を含む）

　　・Log、Exp やべき乗等

　　・誤差関数、累積正規分布関数、ガンマ関数等

　　・線形畳み込み（Convolution）・相関演算（Correlation）

線形畳み込み・相関演算について

線形畳み込み（Convolut(VectorDenseDouble, VectorDenseDouble, VectorDenseDouble)）や Convolut(VectorDenseComplex, VectorDenseComplex, VectorDenseComplex)）） と全く同じ処理を C# で単純に記述すると以下のようになります（ベクトルは double で配列のインデックスは１から開始する例です）。

コードをコピー

// // _VML.Convolut() と全く同じように動作する単純な線形畳み込み演算メソッド. // y[r] = Σx1[t]・x2[r-t] を可能な全ての t に対して実行します. // public VectorDenseDouble LasyConvlut(VectorDenseDouble y, VectorDenseDouble x1, VectorDenseDouble x2) { int pmax = x1.Count; int qmax = x2.Count; int rmin = 2; int rmax = pmax + qmax; if (y == null || y.Count >= x1.Count + x2.Count) y = new VectorDenseDouble(x1.Count + x2.Count - 1); for (int r = rmin; r <= rmax; ++r) { int tmin = Math.Max(1,r - qmax); int tmax = Math.Min(pmax,r - 1); if (tmin > tmax) continue; double s = 0; for (int t = tmin; t <= tmax; ++t) { s += x1[t] * x2[r - t]; } y[r - rmin + 1] = s; } return y; }

同様に線形相関（Correlat(VectorDenseDouble, VectorDenseDouble, VectorDenseDouble)）や Correlat(VectorDenseComplex, VectorDenseComplex, VectorDenseComplex)）） の処理は以下のようになります。

コードをコピー

// // _VML.Correlat() と全く同じように動作する単純な線形相関演算メソッド. // y[r] = Σx1[t]・x2[r+t] を可能な全ての t に対して実行します. // public VectorDenseDouble LasyCorrelat(VectorDenseDouble y, VectorDenseDouble x1, VectorDenseDouble x2) { int pmax = x1.Count; int qmax = x2.Count; int rmin = 1 - pmax; int rmax = qmax - 1; if (y == null || y.Count >= x1.Count + x2.Count) y = new VectorDenseDouble(x1.Count + x2.Count - 1); for (int r = rmin; r <= rmax; ++r) { int tmin = Math.Max(1, 1 - r); int tmax = Math.Min(pmax, qmax - r); if (tmin > tmax) continue; double s = 0; for (int t = tmin; t <= tmax; ++t) { s += x1[t] * x2[r + t]; } y[r - rmin + 1] = s; } return y; }

もちろん実際の計算はマルチスレッド化やFFTと同様なロジックを用いて複雑な処理が実行されます。 上記のコードと _VML の処理時間を比較してみると（比較になりませんが…）、_VML が如何に高速であるか理解できると思います。

数値で与えられた n 個のデータ点列 (x_i,y_i(x_i)) (i=1,2,...,n) の n-1 個の区間（x_i < x_i+1） (i=1,2,...,n-1) を多項式（n-1個）で結ぶ多項式スプライン（以後単にスプラインと呼びます）のクラスです。各多項式は同じ次数で各項の係数だけが異なるものとします。 この多項式に基づいて任意の点 x の y(x) （補間）や任意範囲の積分値を計算することができます。

Mol ではデータ点列を保持し補間や積分の計算を実行する DataFitting クラスと _Spline から派生した各種の多項式クラス（０次：SplineStepWise、１次：SplineLinear、 ２次：SplineQuadratic、３次：SplineCubic）が用意されています。 まず、データ点列を引数にしてDataFittingクラスを作成し、次に多項式クラスを作成してDataFittingオブジェクトにセットします。

各区間の多項式(P_i(x))は基本的に以下のような形になります（i は区間番号）。

P_i(x) = C_i,0 + C_i,1(x - x_i)¹ + ... + C_i,k(x - x_i)^k ただし x_i ≤ x ≤ x_i+1

ここで C_i,j は i 番目の区間の多項式（P_i(x)）の j 次の項の係数（定数）。 k は多項式の（最大）次数となります( 0 ≤ j ≤ k )。さらに x は x_i ≤ x ≤ x_i+1 （i=1,2,...,n-1) となります。任意に与えられた x がどの区間にあるかを検索して得られた区間の P_i(x) を y(x) の近似として使用します。

一般に 3 次式以上は計算が複雑になり結果も不安定になるので Mol で利用できる次数 k は　0 ～ 3 です。

さて、P_i(x) には k+1 個の係数があり、 y(x) の近似として利用するには、この全係数を決定する必要があります。 (n-1)個の区間に(k+1)個の係数があるので全係数は (n-1)・(k+1) 個になります。従って同じ数だけの方程式が必要になります。 各区間の両端点の値はデータで与えられていますので方程式は最低で 2・(n-1) 個あります。その他の方程式は各接点での導関数（(k-1)階までの） が連続であるという条件から与えられます。以下、具体的に Mol で扱う最大の３次スプラインを例に説明します。

計算対象：求める全係数の数

３次の多項式 (k=3) ですので、求める全係数は (n-1)・(k+1) = 4・(n-1) 個となります。

条件１：与えられたデータ

(n-1)個の各多項式の両端点の値は与えられたデータ値と一致するので方程式は 2・(n-1) 個。

条件２：１次導関数

各多項式が交わる境界点（接点）は n-2 個あり、各接点での１次導関数が連続（値が一致する）すると仮定して 方程式は n-2 個。

条件３：２次導関数

各多項式が交わる境界点（接点）は n-2 個あり、各接点での２次導関数が連続（値が一致する）すると仮定して 方程式は n-2 個。

３次式の場合、連続条件はここまでで、全方程式は 2・(n-1) + n-2 + n-2 = 4・n-6 個となります。 一方、未知数（係数）は 4・n-4 個ですので残り２つの方程式があれば全係数を計算することができます。 残りの２つは境界条件（BoundaryCondition）として利用者が与えます。 一般的な境界条件は x₁ と x_n に於ける１次導関数や２次導関数の値（組み合わせることも可） を数値で与えます。数値以外にも以下のような条件を与えることができます（境界値は無視されます）。

NOT_A_KNOT条件

C_1,3 = C_2,3 、 C_n-2,3 = C_n-1,3 先頭と最後の隣り合う多項式に一定の関連性を与える条件です。

FREE_END条件

x₁ と x_n に於ける２次導関数の値がゼロ（値ゼロの２つの２次導関数を指定しても同じです）。 これは、先頭と最後の区間の傾きが一定（曲げのモーメントはゼロ）という条件です。

PERIODIC条件

x₁とx_nに於ける各導関数が等しい周期スプライン条件です。 この場合、与えるデータ点列は y₁=y_n である必要があります。

以上は多項式が３次の場合ですが、その他の多項式も同様に計算できます。 Mol では各多項式に対応するクラスが用意されています。

０次多項式（SplineStepWise）

y_i(x) = C_i,0になります。 多項式の連続性は過剰な条件となり適用されません。従って各接点で y の値は不連続になります。 各区間の２つ端点のうち右か左の、どちらを区間に含めるか指定する必要があります（デフォルトは左）。

１次多項式（SplineLinear）

各区間の端点同士は直線で結ばれます。境界条件はありません。

２次多項式（SplineQuadratic）

各区間の端点同士は２次の多項式で結ばれます。１個の境界条件を与える必要があります。

３次多項式（SplineCubic）

各区間の端点同士は３次の多項式で結ばれます。２個の境界条件を与える必要があります。

Mol でのスプライン計算は以下の手順になります。

１．DataFitting クラスをデータ点列を引数にして作成する。

DataFittingオブジェクトは各データ点列の保有と補間や積分の計算を実行します。

	コードをコピー
VectorDenseDouble x = new VectorDenseDouble(10); VectorDenseDouble y = new VectorDenseDouble(10); // x[] と y[] に値をセット ................. // DataFitting オブジェクトの作成 DataFitting df = new DataFitting(x, y);

y がベクトルなら一つの x_i に対して一つの y_i が対応します。 y に行列（MatrixDenseGeneralDouble）を与えることもできます。その場合、一つの x_i に対して 複数（m個）の y_i,j (j=1,...,m) が対応します。

２．_Spline から派生した多項式クラスを作成してDataFittingオブジェクトにセットする。

	コードをコピー
// ３次スプラインの多項式関数の作成とセット SplineCubic sc = new SplineCubic(); // 多項式に境界条件を設定する（この場合、境界値をセットする必要はない） sc.SetBoundaryCondition(SplineCubic.SINGLE_BOUNDARY_CONDITION.NOT_A_KNOT); // DataFitting オブジェクトに多項式をセットする。 df.SetSpline(sc);

３次スプラインですので領域の左右に於ける導関数を指定することも可能です。

３．DataFittingオブジェクトに指定した多項式に基づいて補間や積分の計算を実行する。

	コードをコピー
// 補間の実行 x=0.7 の位置の y を計算する double y = (double)df.ComputeAt(0.7); // 積分の実行 x=0.1 から 11.0 までの積分を計算する double Y = (double)df.Integrate(0.1, 11.0);

ComputeAtやIntegrateメソッドには上記のようにスカラーを指定できますが、複数の補間や積分を一度に実行するためベクトルを指定することもできます。 各メソッドの戻り値を(double)でキャストしているのは DataFitting オブジェクトの作成時の指定と計算メソッドに指定した内容に応じて メソッドの戻り値がスカラ－、ベクトル、そして行列になり得るからです。

注意事項：
境界点列 xi と xi+1 の値が近いと計算値の誤差が大きくなります。

注意事項：
ComputeAt() や Integrate() に与える x が範囲外（x1～xnの外側）の時は 両端の多項式を使用して計算されますが誤差が非常に大きくなります。

乱数とは「予測も再現もできない数列の値」を生成することです。 確定的な計算によってしか数列を作ることができないコンピューターでは疑似的な乱数（疑似乱数）を生成します。 予測不可能な（非決定的：non-deterministic）な乱数を生成するには専用のハードウェア等が必要になります。 疑似乱数を生成するには線形合同法（乗算合同法・混合合同法）、線形帰還シフトレジスタ法やメルセンヌ・ツイスタ法等がありますが、 詳細はそれぞれの文献などを参照してください。 RandomNumber は各種の疑似乱数発生器を乱数を発生させ、それを、指定された統計分布（連続分布・離散分布）に従った乱数列に変換・生成します。

※確率密度関数や分布関数等についてはリファレンスの「 数式表記」の項を参照してください。

計算手順：

１．RandomNumber クラスを疑似乱数生成方法と初期値（Seed と言います）を引数にして作成する。

	コードをコピー
RandomNumber r = new RandomNumber(GENERATOR.MCG59, 7777);

２．各種分布関数に対応した乱数発生メソッドを呼び出して乱数をベクトルに格納する。

	コードをコピー
VectorDenseDouble y = new VectorDenseDouble(1000); // 平均値 a、標準偏差 sd、でボックスミューラー法を用いて疑似乱数から正規分布に従った乱数を生成して y の全要素に格納します。 r.GenerateGaussian(y, a, sd, GAUSSIAN_METHOD.BOXMULLER);

Statは特に巨大な標本データからさまざまな統計的推定値を計算します。

主な統計量はStatクラスのプロパティとなっています。 もちろん計算対象の標本データ（行列の形で指定します）がなければ計算は始まりませんので、まずは標本データを指定して Stat オブジェクトを作成します。

コードをコピー

int N = 10000; // 標本数：例えば、全生徒数（データの大きさ）。確率的な表現を用いれば全試行回数. int P = 10; // 次元数：例えば　英語の点数、国語の点数、理科の点数…等、同一対象（生徒）から同時に得られる値の数. MatrixDenseGeneralDouble data = new MatrixDenseGeneralDouble(N, P); Stat stat = new Stat(data); // 計算対象の標本データ data を指定して Stat オブジェクトを作成する. ............... data に標本データを読み込む等の処理 ................... // stat は data の参照を stat.DataMatrix プロパティに保持しますので // data を直接扱っても stat.DataMatrix にデータを設定しても結果は同じです。 stat.ComputeProperties(); // 各種統計量の計算

ComputeProperties()メソッドで計算される統計量は以下の通りです。平均値（Mean）は必ず計算されるので参照を設定 する必要はありません（設定できません）が、例えば、分散（Variance）等が必要なら自分で data.Variance にベクトルを設定します。 null を設定すれば「計算する必要が無い」ということになります。または、stat.Computed = Stat.PROPERTIES.VARIANCE; とすれば 自分で設定しなくても（設定してもかまいません）、必要なら stat が内部で自動的にベクトルを作成して data.Variance に設定します。

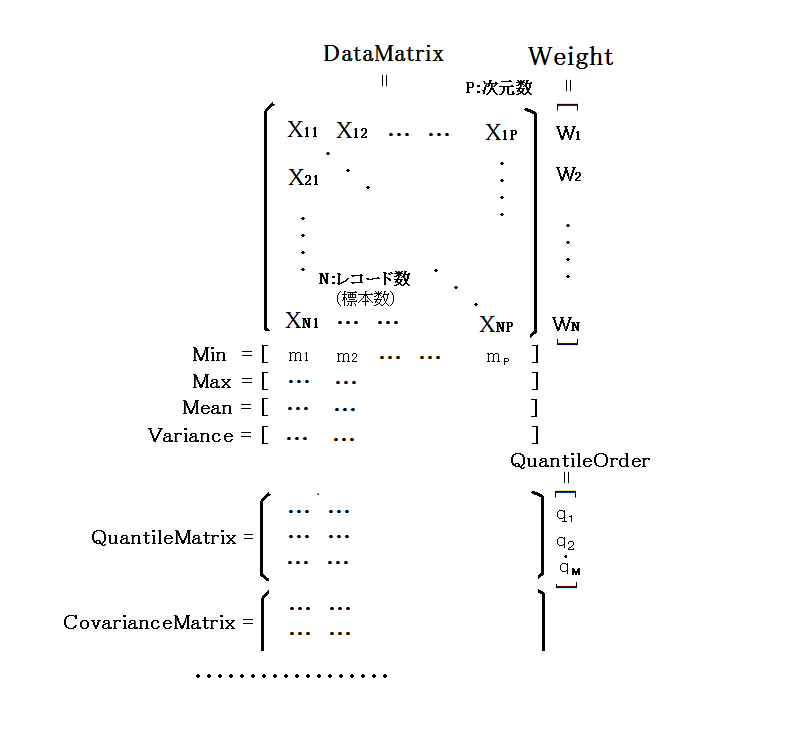
※各プロパティの計算式等についてはリファレンスの「 数式表記」の項を参照してください。

※以下 N は（上記例題と同じで）サンプルデータの数、P は次元（属性）数を意味します。

[巨大データの処理方法]：分割計算

標本数が巨大で全てを DataMatrix に格納するのが難しい場合は、バケツのように DataMatrix （重みが必要な場合は Weight も） の内容を入れ替えて繰り返し ComputeProperties() を実行することで計算することができます。

	コードをコピー
int N = 1000; int P = 10; int i = 0; MatrixDenseGeneralDouble data = new MatrixDenseGeneralDouble(N,P); Stat stat = new Stat(data); while(GetDataChunk(stat)) { stat.ComputeProperties(i++); }

ここで、GetDataChunk()メソッドはファイルやデータベースから最大 N レコード（重みがあれば重みも）を stat.DataMatrix に読み込んで true を返すものとします。レコードの残りが N より少ないときは stat.DataMatrix 自体を再設定（小さいバケツに取り換える）してからデータを読み込みます。 全く読み込むデータが無い場合は false を返します。

重要な注意事項：
最初の ComputeProperties() の呼び出しは、必ず引数の値をゼロ（ stat.ComputeProperties(0) ）にしなければなりません（その後はゼロ以外に）。

分割計算では分位値以外（平均値等）のプロパティは正確に計算されます。 分位値（QuantileMatrix）は全データをソートしてからでないと正確に計算できないので、分割計算では推定値になります。 一括計算で正確な分位値を計算することもできます。

一括計算

一括計算は DataMatrix に全てのデータが格納されていることを前提にします。 分割計算ではサポートされない、以下のような DataMatrix に対する高度な計算が実装されています。

色々なタイプの行列は主に連立方程式 A*x = b を効率よく解くために考え出されたものです。 ここで A は係数行列で、様々な行列を指定することができます。b は密な定数ベクトルです。 同じ係数行列 A を用いて異なる定数ベクトルを複数指定することもできます。この時は b は密な一般行列になります。 x は計算結果としての解ベクトルになります（b　が行列の場合は x も同じサイズの行列になります）。 連立方程式を解く場合、まず、行列 A を因子分解します。因子分解が完了すれば、LuSolver オブジェクトの Solve() メソッドに定数項（一般にはベクトルですが、 行列を与えて一度に複数の定数項を与えることもできます）を与えて連立方程式を繰り返し説くことができます。 以下のように２ステップになります。

	コードをコピー
LuSolver lu = LuSolver.Create(A); // A を因子分解する（A の性質により因子分解法が選択されます）. VectorDenseDouble x = lu.Solve(b); // 因子分解の結果(luが保持します)を用いて連立方程式を解きます.

最も基本的な因子分解は A => L*U と A を L(下三角行列) と U(上三角行列) の積に分解します。しかし、A が正定値や半正定値対称行列の場合、 L のみを計算すること等で大幅に計算時間を短縮することができます。 三角行列のように因子分解の必要が無いものもあります（いずれの場合でもLuSolver.Create(A)のステップは必要です）。

行列 A が一般行列（正定値性が不明なもの）なら LU分解、正定値対称行列なら Cholesky分解、 半正定値対称行列なら修正Cholesky分解 (Bunch-Kaufman 分解)が使用されます。 計算時間は

LU分解 > 修正Cholesky分解 > Cholesky分解

の順になります。

対称行列の場合「正定値」であると予め分っている場合は UserTypeプロパティに USER_TYPE.USER_MATRIX_POSITIVE (_Mol..::..USER_TYPE) を設定すれば Cholesky分解 が、そうでない場合は 修正Cholesky分解 が適用されます。

一般行列は全ての型の行列を格納できます。何も指定しなければ LU分解が選択されますが、 UserTypeプロパティに、対称性や三角性等 (_Mol..::..USER_TYPE)を積極的に指定することで効率よく解くことができます。 対称性や上三角の性質を指定すると下三角部分はアクセスされません。下三角性を指定すれば上三角部分がアクセスされなくなります。

当然ながら間違った設定は間違った答えを得ることになります。 因子分解の結果は LuSolver オブジェクトが保持します。使用メモリーを減らすために、指定によって元の行列 A に結果を格納することも可能です。 この場合、Solve メソッド実行前に A の内容を変更してしまうと当然間違った結果を得ることになります。

注意事項：
行列の正定値性や因子分解についての詳細は省略します。それぞれの文献等を参照してください。

線形連立方程式解法のパターン

全ての行列に対応しているため、複雑に見えますが、解法のパターンは以下のようにまとめられます（Create()はクラスメソッド、Solve()はインスタンスメソッドであることに注意してください）。 LuSolverについてはレファレンスを参照してください。

線形最小二乗問題(LLS)とは、行列 A(サイズ：m x n) と ベ クトル b が与えられたときに、二乗和Σ_i((Ax)_i - b_i)₂ を最小にするベクトル x を見つけることです。 m ≥ n で rank(A) = n ならば、優決定の連立 1 次方程式 ( 未知数より方程式の個数の方が多い) に対して最小二乗解を見つけることで 、行列 A のQR 因子分解を使用します。

m < n で rank(A) = m の場合は、Ax = b を満たす ( つまり、ノルム||Ax − b||₂ が最小になる) 解 x は無限に存在します。 これは、劣決定の連立 1 次方程式 (方程式より未知数の個数の方が多い)に対して最小ノルム解（||x||₂ を最小にする x ）を見つけることになります。 この問題を解くには、行列 A のLQ 因子分解を使用します。

Rank = min(m,n) の場合は最大階数ですが、 一般には、A の階数が不明 rank(A) < min(m, n) であり、階数不足の最小二乗問題になります。この場合は ||x||₂ も ||Ax − b||₂ も最小にする最小ノルム最小二乗解を見つけます。 解法は、QR 因子分解 と、ピボット演算または特異値分解を併用します。

※各種因子分解の詳細については、それぞれの文献等を参照してください。

LlsSolver クラスは基本的な演算はスタティックメソッドで実行します。 各メソッドで作成されるインスタンス LlsSolver は計算の結果として得られる 特異値や階数を保持しますが、解ベクトルなどは引数で指定するようになっています。計算中に作成された作業変数を解放するために Dispose() メソッドを 積極的に呼び出すようにしてください。

※現時点の線形最小二乗計算では疎な行列はサポートしていません。

※線形最小二乗計算の結果として、行列 A の階数や特異値ベクトルが計算されます（解法によっては計算されないこともあります）。

線形最小二乗問題解法のメソッド

全てのメソッドはクラスメソッドです。実数や複素数の行列やベクトルの指定で数はかなりありますが、以下のようにパターンに分類されます。

※LlsSolver.SolveLSE(x,A,B,c,d)メソッドだけは特殊（戻り値は解ベクトル）で 均衡制約を持つ線形最小二乗 (LSE) 問題 minimize || c - A x ||₂ を解きます。ただ し、Bx = d で A は m × n の行列、B は p × n の行列、c は与えられたm- ベクトル、d は与えられたp- ベクトル。 さらに、p ≤ n ≤ m+p、で Rank(B) = p、Rank(A｜B) = n を仮定します（A｜B は A と B を上下に並べた行列とします）。

A を (m × n) の一般行列として、A の特異値分解 (SVD) とは A = UΣV^H の形に分解することです（V^Hは行列 V の複素共役転置）。 ここで、U (m × m) と V (n × n) は、ユニタリ行列 (A が複素行列の場合) または直交行列 (Aが実行列の場合)です。

Σ は、次に示す対角成分σ_i を持つ m × n の対角行列（対角要素のみの帯行列で代用します）になります。

σ₁ ≥ σ₂ ≥ ... ≥ σ_{min(m, n)} ≥ 0

※ σ_i は A の特異値。また、非ゼロの特異値の個数は A の階数(Rank)となります。

※ σ_i は実数です。ただし A が複素数行列の時は Σ も全ての要素の虚数部がゼロの複素数帯行列となります。

A の条件数（Condition number）は 最大特異値 / 最小特異値 で表現可能です。 行列 U と V の先頭から min(m, n) の列は、それぞれ、A の左特異ベクトルと右特異ベクトルとなります。 対応する特異値と特異ベクトルは、Av_i = σ_iu_i かつ A^Hu_i = σ_iv_i

を満たします。ここで u_i と v_i は、 それぞれ、U と V の i 番目の成分です。

※現時点の特異値分解計算では疎な行列はサポートしていません。

※計算では V ではなく V^H（V の複素共役転置）が得られることに注意。 　従って、 Av_i = σ_iu_i を計算する場合は、計算結果の複素共役転置を実行して本来の V に戻すことが必要です （Av の v は計算結果 V の複素共役転置後の列ベクトル）。

※得られる特異値は（対角要素のみの）帯行列の対角要素に格納されます。

特異値分解計算のメソッド

全てのメソッドはクラスメソッドです。実数や複素数の行列やベクトルの指定で数はかなりありますが、以下のようにパターンに分類されます。

固有値問題解法とは、行列 A が与えられたときに、以下の式を満たす固有値 λ と、対応する固有ベクトル x を計算します。

Ax_i = λ_ix_i : 標準固有値問題

Ax_i = λ_iBx_i: 汎用固有値問題 (A と B は同じタイプの行列で、かつ、B は正定値である必要があります)。

λ と x は A の列（行）の数だけあります。従って、固有値λ はベクトル、固有ベクトル x は行列（列 i が x_i に対応します）の形で計算されます。 A が実数対称行列、またはエルミート行列の場合、λ は実数（Aが複素数なら虚数部がゼロの複素数）になります。 x は A が複素数なら複素数一般行列になります。

実数（Aが複素数なら虚数場がゼロ）固有値を計算するので、対象とする行列は対称行列かエルミート行列です。 ただし、計算の効率を考慮して一般行列（または帯行列）の各要素が対称（またはエルミート）的に格納されていると見なして計算することもできます。 この場合、対称性を仮定して、対角要素を含めた上半分の要素だけが計算に使用されます。

固有値問題計算のメソッド

最初に呼び出すメソッド（Solve／Solve2）はクラスメソッドです。正常に固有値が計算できればEgvSolverオブジェクトが得られます。 目的とする固有値や固有ベクトルは EgvSolver オブジェクトのプロパティとして得られます。 実数や複素数の行列やベクトルの指定で数はかなりありますが、以下のようにパターンに分類されます。

非線形連立方程式を扱う、NonlinearEquationsオブジェクトは、以下の機能を提供します。 以下、各連立方程式を F_i(X₁,X₂,...,X_n) {ただし、i=1,2,...,m} と 記述します。 また、同じ F を各方程式の関数値を保持する実数ベクトル、X を独立変数ベクトルの意味にも用います。 　さらに m は F の要素数（連立方程式の数）、n を X の要素数（独立変数の数）とします。

　・連立方程式を計算して、各関数値をベクトル要素にセットして返す（ComputeEquations()メソッド、F <= X）

　・ヤコビー行列の計算（ComputeJacobian()メソッド、∂F_i/∂X_j： 行 i=1,2,...,m 列 j=1,2,...,n）

　・連立方程式のユークリッドノルム値、S = (Σ_i(F_i(X))²)^1/2　{i=1,2,...,m}、 の最小化（MinimizeNorm()メソッド、非線形連立方程式の最小二乗問題）の計算。

注意事項：
非線形連立方程式の最小二乗問題の特別なケースとして、 m=n で S=>0 となる場合は、非線形連立方程式を解くことになります。

基本的なプログラミングは、ベクトル F を計算する式を NonlinearEquations オブジェクトに提供して、上記メソッドを呼び出すだけです。

F を計算する式を NonlinearEquations オブジェクトに設定する方法は以下の２通りあります。

各実装方法等は例題に詳述されていますので、ダウンロードして参照してください。

非線形最小二乗問題を、MinimizeNorm()メソッドで、解くには以下の手法が用意されています。

注意事項：
最小二乗問題で使用する収束判定定数は複数設定可能です。MinimumTrustRegion、MinimumNorm、MinimumYacobianNorm、MinimumTrialStep、MinimumNormChange等のプロパティ値を 設定して収束状態を調節してください。

参照

その他のリソース